题目内容
 如图所示的多面体中,EF丄平面AEB,AE丄EB,AD∥EF,BC∥EF,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点
如图所示的多面体中,EF丄平面AEB,AE丄EB,AD∥EF,BC∥EF,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点
(1)求证:BD丄EG;
(2)求平面DEG与平面DEF所成二面角的大小.
 (1)证明:∵EF丄平面AEB,AE?平面AEB,BE?平面AEB
(1)证明:∵EF丄平面AEB,AE?平面AEB,BE?平面AEB∴EF⊥AE,EF⊥BE
∵AE丄EB,∴EB,EF,EA两两垂直
以点E为坐标原点,EB,EF,EA分别为x,y,z,建立如图所示的空间直角坐标系,则E(0,0,0),B(2,0,0),D(0,2,2),G(2,2,0)
∴
 ,
,
∴

∴BD丄EG;
(2)解:已知得
 是平面DEF的法向量
是平面DEF的法向量设平面DEG的法向量为
 ,∵
,∵ ,
,
∴
 ,∴可取
,∴可取
设平面DEG与平面DEF所成二面角θ
∴
 =
=
∴平面DEG与平面DEF所成二面角为
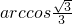 .
.分析:(1)先证明EB,EF,EA两两垂直,以点E为坐标原点,EB,EF,EA分别为x,y,z,建立空间直角坐标系,证明
 ,即可证明BD丄EG;
,即可证明BD丄EG;(2)
 是平面DEF的法向量,平面DEG的法向量为
是平面DEF的法向量,平面DEG的法向量为 ,利用数量积公式,即可得到平面DEG与平面DEF所成二面角.
,利用数量积公式,即可得到平面DEG与平面DEF所成二面角.点评:本题考查线线垂直,考查面面角,解题的关键是建立空间直角坐标系,利用坐标表示向量,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
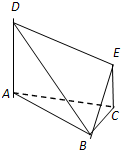 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1. 在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABCD是菱形.
在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABCD是菱形. (2011•盐城二模)在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABCD是菱形.
(2011•盐城二模)在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABCD是菱形. 如图所示的多面体中,EF丄平面AEB,AE丄EB,AD∥EF,BC∥EF,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点
如图所示的多面体中,EF丄平面AEB,AE丄EB,AD∥EF,BC∥EF,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点 如图所示的多面体中,正方形BB1C1C所在平面垂直平面ABC,△ABC是斜边
如图所示的多面体中,正方形BB1C1C所在平面垂直平面ABC,△ABC是斜边