题目内容
函数y=ax-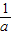
（a＞0，a≠1）的图象可能是（ ）A．
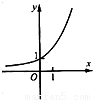
B．
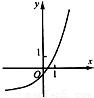
C．
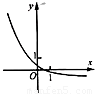
D．
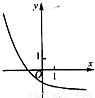
【答案】分析：讨论a与1的大小，根据函数的单调性，以及函数恒过的定点进行判定即可．
解答：解：函数y=ax-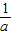
（a＞0，a≠1）的图象可以看成把函数y=ax的图象向下平移
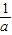个单位得到的．
当a＞1时，函数y=ax-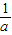
在R上是增函数，且图象过点（-1，0），故排除A，B．
当1＞a＞0时，函数y=ax-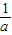
在R上是减函数，且图象过点（-1，0），故排除C，
故选D．
点评：本题主要考查了指数函数的图象变换，指数函数的单调性和特殊点，体现了分类讨论的数学思想，属于基础题．
解答：解：函数y=ax-
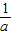（a＞0，a≠1）的图象可以看成把函数y=ax的图象向下平移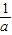个单位得到的．当a＞1时，函数y=ax-
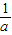在R上是增函数，且图象过点（-1，0），故排除A，B．当1＞a＞0时，函数y=ax-
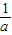在R上是减函数，且图象过点（-1，0），故排除C，故选D．
点评：本题主要考查了指数函数的图象变换，指数函数的单调性和特殊点，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
已知函数y=f（x）的图象与函数y=ax（a＞0且a≠1）的图象关于直线y=x对称，记g（x）=f（x）[f（x）+f（2）-1]．若y=g（x）在区间[
，2]上是增函数，则实数a的取值范围是（ ）
| 1 |
| 2 |
| A、[2，+∞） | ||
| B、（0，1）∪（1，2） | ||
C、[
| ||
D、(0，
|