题目内容

已知正项数列{an} 满足a1=a(0＜a＜1＝,且an+1=.求证:

(1)0＜an+1＜；

(2)an=;

(3)+…+＜1.

证明：(1)∵y=,

∴函数y=(0＜x＜1)是增?函数.

由已知an+1=,0＜an＜1,

∴0＜an+1＜.

(2)∵an+1=(n∈N*),

∴1(n∈N*),

即数列{}是首项为,公差为1的等差数列.

∴=+(n-1),an=(n∈N*).

(3)由已知an=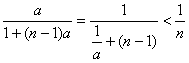(∵0＜a＜1),

∴+…++…+

=1-＜1.

练习册系列答案
相关题目
已知正项数列{an}满足：a1=3，（2n-1）an+2=（2n+1）an-1+8n2（n＞1，n∈N*）
（1）求证：数列{
an
2n+1
}为等差数列，并求数列{an}的通项an．
（2）设bn=
1
an
，求数列{bn}的前n项和为Sn，并求Sn的取值范围．
定义：称
n
a1+a2+…+an
为n个正数a1，a2，…，an的“均倒数”，已知正项数列{an}的前n项的“均倒数”为
1
2n
，则
lim
n→∞
nan
sn
（　　）
A、0
B、1
C、2
D、
1
2
已知正项数列an中，a1=2，点(
an
，an+1)在函数y=x2+1的图象上，数列bn中，点（bn，Tn）在直线y=-
1
2
x+3上，其中Tn是数列bn的前项和．（n∈N+）．
（1）求数列an的通项公式；
（2）求数列bn的前n项和Tn．
已知正项数列{an}满足a1=1，an+1=an2+2an（n∈N+），令bn=log2（an+1）．
（1）求证：数列{bn}为等比数列；
（2）记Tn为数列{
1
log2bn+1•log2bn+2
}的前n项和，是否存在实数a，使得不等式Tn＜log0.5(a2-
1
2
a)对?n∈N+恒成立？若存在，求出实数a的取值范围；若不存在，请说明理由．
已知正项数列{an}，Sn=
1
8
(an+2)2
（1）求证：{an}是等差数列；
（2）若bn=
1
2
an-30，求数列{bn}的前n项和．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网