题目内容
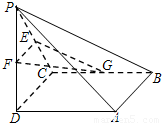 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为PC、PD、BC的中点.(1)求证:PA⊥EF;
(2)求二面角D-FG-E的余弦值.
【答案】分析:(1)以D为原点,建立如图所示的空间直角坐标系D-xyz,求出各顶点的坐标及直线与PA与EF的方向向量,然后代入向量数量积公式,易得两个向量的数量积为0,故PA⊥EF;
(2)在(1)中所示的坐标系中,我们求也平面DFG和平面EFG的法向量,然后代入二面角的向量法夹角公式中,即可得到二面角D-FG-E的余弦值.
解答: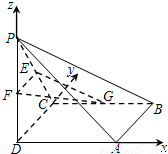 证明:(1)以D为原点,建立如图所示的空间直角坐标系D-xyz,
证明:(1)以D为原点,建立如图所示的空间直角坐标系D-xyz,
则F(0,0.1),E(0,1,1),P(0,0,2),A(2,0,0),
∴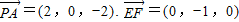 、
、
∵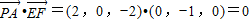 ,
,
∴PA⊥EF
解:(2)D(0,0,0),F(0,0,1),G(1,2,0),
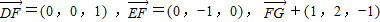 =(1,2,-1)
=(1,2,-1)
设平面DFG的法向量为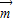 =(x1,y1,z1),
=(x1,y1,z1),
∵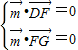
∴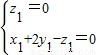
令y1=1,得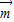 =(-2,1,0)是平面DFG的一个法向量、
=(-2,1,0)是平面DFG的一个法向量、
设平面EFG的法向量为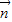 =(x2,y2,z2),
=(x2,y2,z2),
∴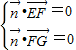 ∴
∴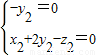
,令z2=1,得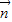 =(1,0,1)是平面EFG的一个法向量、
=(1,0,1)是平面EFG的一个法向量、
∵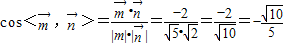
设二面角D-EG-E的平面角为θ,
则θ=<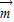 ,
,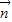 >、
>、
所以二面角D-FG-G的余弦值为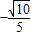
点评:本题考查的知识点是直线与平面垂直的性质及二面角的平面角及求法,空间向量法解决夹角问题的其步骤是:建立空间直角坐标系⇒明确相关点的坐标⇒明确相关向量的坐标⇒通过空间向量的坐标运算求解.
(2)在(1)中所示的坐标系中,我们求也平面DFG和平面EFG的法向量,然后代入二面角的向量法夹角公式中,即可得到二面角D-FG-E的余弦值.
解答:
 证明:(1)以D为原点,建立如图所示的空间直角坐标系D-xyz,
证明:(1)以D为原点,建立如图所示的空间直角坐标系D-xyz,则F(0,0.1),E(0,1,1),P(0,0,2),A(2,0,0),
∴
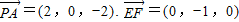 、
、∵
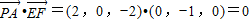 ,
,∴PA⊥EF
解:(2)D(0,0,0),F(0,0,1),G(1,2,0),
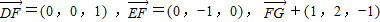 =(1,2,-1)
=(1,2,-1)设平面DFG的法向量为
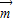 =(x1,y1,z1),
=(x1,y1,z1),∵
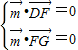
∴
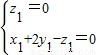
令y1=1,得
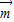 =(-2,1,0)是平面DFG的一个法向量、
=(-2,1,0)是平面DFG的一个法向量、设平面EFG的法向量为
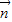 =(x2,y2,z2),
=(x2,y2,z2),∴
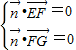 ∴
∴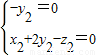
,令z2=1,得
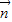 =(1,0,1)是平面EFG的一个法向量、
=(1,0,1)是平面EFG的一个法向量、∵
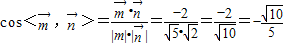
设二面角D-EG-E的平面角为θ,
则θ=<
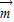 ,
,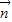 >、
>、所以二面角D-FG-G的余弦值为
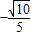
点评:本题考查的知识点是直线与平面垂直的性质及二面角的平面角及求法,空间向量法解决夹角问题的其步骤是:建立空间直角坐标系⇒明确相关点的坐标⇒明确相关向量的坐标⇒通过空间向量的坐标运算求解.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点. 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4, 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.