题目内容
(本小题满分12分)
某工厂拟建一座平面图为矩形且面积为200平方米的三级污水处理池(平面图如图)。由于地形限制,长、宽都不能超过16米。如果池外圈四周壁造价为每平方米400元,中间两条隔墙造价为每平方米248元,池底造价为每平方米80元,池壁的厚度不计。试设计污水处理池的长和宽,使总造价最低,并求出最低总造价。(池深用h 表示)

某工厂拟建一座平面图为矩形且面积为200平方米的三级污水处理池(平面图如图)。由于地形限制,长、宽都不能超过16米。如果池外圈四周壁造价为每平方米400元,中间两条隔墙造价为每平方米248元,池底造价为每平方米80元,池壁的厚度不计。试设计污水处理池的长和宽,使总造价最低,并求出最低总造价。(池深用h 表示)

当 时,y 有最小值 为 16000+29000h 元。
时,y 有最小值 为 16000+29000h 元。
 时,y 有最小值 为 16000+29000h 元。
时,y 有最小值 为 16000+29000h 元。解:设长为x米,则宽为 米,总造价为y元
米,总造价为y元

由 得
得 
因为 在
在 上是减函数,
上是减函数,
所以当 时,y 有最小值 为 16000+29000h 元。
时,y 有最小值 为 16000+29000h 元。
 米,总造价为y元
米,总造价为y元
由
 得
得 
因为
 在
在 上是减函数,
上是减函数,所以当
 时,y 有最小值 为 16000+29000h 元。
时,y 有最小值 为 16000+29000h 元。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
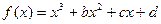 在(0,+
在(0,+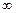 )上是增函数,在[–1,0]上是减函数,且方程
)上是增函数,在[–1,0]上是减函数,且方程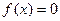 有三个根,它们分别为α,–1,β.
有三个根,它们分别为α,–1,β.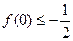 ;
;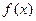 的定义域为R,对任意的
的定义域为R,对任意的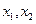 都满足。
都满足。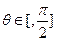 时,不等式
时,不等式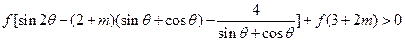
 恒成立,如存在,求出m的取值范围;若不存在,说明理由。
恒成立,如存在,求出m的取值范围;若不存在,说明理由。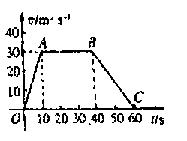
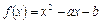 的两个零点是2和3,则函数
的两个零点是2和3,则函数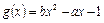 的零点是( )
的零点是( )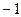 和
和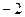
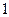 和
和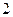
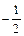 和
和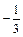
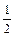 和
和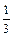



 在区间
在区间 上的零点个数为 ( )
上的零点个数为 ( ) ,
, 为两个不相等的实数,集合
为两个不相等的实数,集合 ,
,  ,映射
,映射 表示把集合
表示把集合 中的元素
中的元素 映射到集合
映射到集合 中仍为
中仍为 等于 ( )
等于 ( ) 相同的函数是( )
相同的函数是( )


