题目内容
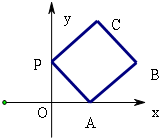
如图，边长为a的正方形组成的网格中，设椭圆C1、C2、C3的离心率分别为e1、e2、e3，则
- A.e1=e2＜e3
- B.e2=e3＜e1
- C.e1=e2＞e3
- D.e2=e3＞e1
D
分析：由图形可知，椭圆C1、C2、C3的长半轴长，短半轴长，分别计算离心率，即可求得结论．
解答：由图形可知，椭圆C1的长半轴长为2a，短半轴长为1.5a，则e1=
=
椭圆C2的长半轴长为4a，短半轴长为2a，则e2=
=
椭圆C3的长半轴长为6a，短半轴长为3a，则e2=
=
∴e2=e3＞e1，
故选D．
点评：本题考查椭圆的几何性质，考查学生的计算能力，属于基础题．
分析：由图形可知，椭圆C1、C2、C3的长半轴长，短半轴长，分别计算离心率，即可求得结论．
解答：由图形可知，椭圆C1的长半轴长为2a，短半轴长为1.5a，则e1=
=椭圆C2的长半轴长为4a，短半轴长为2a，则e2=
=椭圆C3的长半轴长为6a，短半轴长为3a，则e2=
=∴e2=e3＞e1，
故选D．
点评：本题考查椭圆的几何性质，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
（北京卷理14）如图放置的边长为1的正方形PABC沿x轴滚动．设顶点p（x，y）的轨迹方程是y=f（x），则f（x）的最小正周期为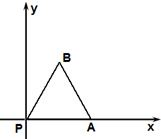
如图放置的边长为1的正三角形PAB沿x轴滚动，设顶点A（x，y）的纵坐标与横坐标的函数关系式是y=f（x），则f（x）在区间[-2，1]上的解析式是
如图放置的边长为1的正方形PABC沿x轴滚动．设顶点p（x，y）的轨迹方程是y=f（x），设f（x）的最小正周期为T，y=f（x）在其两个相邻零点间的图象与x轴所围区域的面积为S，则ST=
（2011•洛阳一模）如图放置的边长为1的正三角形ABC沿x轴的正方向滚动，设顶点A（x，y）的纵坐标与横坐标的函数关系是y=f（x）．则f（x）在两个相邻零点间的图象与x轴围成的面积是
B．
C．
D．
