题目内容
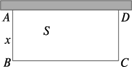
如图所示：用篱笆围成一个一边靠墙的矩形菜园 ，假设墙有足够长．
(Ⅰ) 若篱笆的总长为
，则这个矩形的长，宽各为多少时，菜园的面积最大？
(Ⅱ) 若菜园的面积为
，则这个矩形的长，宽各为多少时，篱笆的总长最短？
解：设这个矩形的长为
，宽为
，篱笆的长为
，面积为
．
(Ⅰ) 由题知
，由于
，
∴
，
，即
，当且仅当
时等号成立．
由
故这个矩形的长为
，宽为
时，菜园的面积最大．
(Ⅱ) 条件知
，
.
,当且仅当时等号成立．
由
故这个矩形的长为
、宽为
时，可使篱笆的总长最短．
练习册系列答案
相关题目
，则这个矩形的长，宽各为多少时，菜园的面积最大？
，则这个矩形的长，宽各为多少时，篱笆的总长最短？
，则这个矩形的长，宽各为多少时，菜园的面积最大？
，则这个矩形的长，宽各为多少时，篱笆的总长最短？
，则这个矩形的长，宽各为多少时，菜园的面积最大？
，则这个矩形的长，宽各为多少时，篱笆的总长最短？