题目内容
经过椭圆 的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,则
的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,则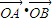 等于 .
等于 .
【答案】分析:由椭圆 可求椭圆的焦点为F(±1,0),不妨设所作直线l过焦点(1,0),故可得直线L:y=x-1,联立
可求椭圆的焦点为F(±1,0),不妨设所作直线l过焦点(1,0),故可得直线L:y=x-1,联立 可求A,B.然后由
可求A,B.然后由 =x1x2+y1y2,代入可求
=x1x2+y1y2,代入可求
解答:解:∵椭圆 中a=
中a= ,b=1
,b=1
∴c=1
椭圆的焦点为F(±1,0)
不妨设所作倾斜角为45°的直线l过焦点(1,0),故直线L:y=x-1
联立 消去y可得,3x2-4x=0
消去y可得,3x2-4x=0
解方程可得,
代入直线y=x-1可得,y1=-1,
 =x1x2+y1y2=
=x1x2+y1y2=
故答案为:
点评:本题主要考查了椭圆性质的应用,直线与椭圆的相交关系的应用,向量数量积的坐标表示等知识的综合应用,属于综合性试题
 可求椭圆的焦点为F(±1,0),不妨设所作直线l过焦点(1,0),故可得直线L:y=x-1,联立
可求椭圆的焦点为F(±1,0),不妨设所作直线l过焦点(1,0),故可得直线L:y=x-1,联立 可求A,B.然后由
可求A,B.然后由 =x1x2+y1y2,代入可求
=x1x2+y1y2,代入可求解答:解:∵椭圆
 中a=
中a= ,b=1
,b=1∴c=1
椭圆的焦点为F(±1,0)
不妨设所作倾斜角为45°的直线l过焦点(1,0),故直线L:y=x-1
联立
 消去y可得,3x2-4x=0
消去y可得,3x2-4x=0解方程可得,

代入直线y=x-1可得,y1=-1,

 =x1x2+y1y2=
=x1x2+y1y2=
故答案为:

点评:本题主要考查了椭圆性质的应用,直线与椭圆的相交关系的应用,向量数量积的坐标表示等知识的综合应用,属于综合性试题

练习册系列答案
相关题目
 的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,则
的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,则 等于 .
等于 . 的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,则
的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,则 等于 .
等于 .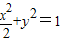 的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,则
的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,则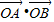 等于 .
等于 . 的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,则
的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,则 等于 .
等于 .