题目内容
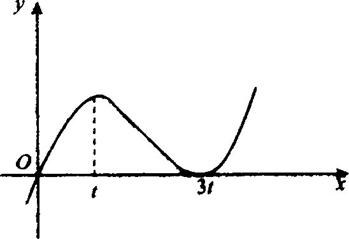
三次函数f(x)=x3+bx2+cx+d的图像大致如图所示,图中的实数t满足(1)试求c、d的值(或用t表示).
(2)试用t表示f(x)在区间[1,2]上的最值;
(3)若不等式t2-mt>f(x)在x∈[1,2]时恒成立,求实数m的取值范围.
第21题图
答案:(1)f′(x)=3x2+2bx+c.

第21题图
由图知,t与3t是函数f(x)的极值点.∴t与3t是方程3x2+2bx+c=0的两根.
于是,t+3t=![]() b=-6t;t·3t=
b=-6t;t·3t=![]() c=9t2;
c=9t2;
f(0)=0![]() d=0.
d=0.
(2)f(x)=x3-6tx2+9t2x.
∵![]() ≤t≤1
≤t≤1![]() [1,2]
[1,2]![]() [t,3t].
[t,3t].
∴f(x)在[1,2]上递减.
于是,f(x)max=f(1)=1-6t+9t2;f(x)min=f(2)=8-24t+36t2.
(3)“t2-mt>f(x)在x∈[1,2]时恒成立”等价于t-mt>f(x)max=1-6t+9t2.
∵t>0,∴m<6-(8t+![]() ).
).
令φ(t)=6-(8t+![]() )(
)(![]() ≤t≤1).
≤t≤1).
则φ(t1)-φ(t2)=[6-(8t1+![]() )]-[6-(8t2+
)]-[6-(8t2+![]() )]=(t1-t2)(
)]=(t1-t2)(![]() -8)
-8)
设![]() ≤t1<t2≤1,则t1-t2<0,
≤t1<t2≤1,则t1-t2<0,![]() -8<0.
-8<0.
∴φ(t1)>φ(t2)![]() φ(t)在[
φ(t)在[![]() ,1]上递减.
,1]上递减.
从而φ(t)min=φ(![]() )=6
)=6![]() .
.
故m<![]() .
.

练习册系列答案
相关题目