题目内容
已知集合P={(x,y)|y=
}、Q={(x,y)|y=x+b},若P∩Q≠∅,则b的取值范围是( )
| 9-x2 |
分析:集合P中的函数解析式表示以原点为圆心,3为半径的半圆上点集;集合Q的函数表示直线y=x+b上的点集,画出两函数图象,如图所示,找出直线y=x+b过(3,0)以及直线y=x+b与半圆相切时的b值,即可确定出b的范围.
解答: 解:根据题意画出函数y=
解:根据题意画出函数y=
与y=x+b的图象,如图所示,
当直线y=x+b过(3,0)时,可得b=-3;
当直线y=x+b与圆相切时,圆心(0,0)到直线的距离d=r=
=3,
解得:b=3
或b=-3
(舍去),
则P∩Q≠∅时b的取值范围是-3≤b≤3
.
故选C
 解:根据题意画出函数y=
解:根据题意画出函数y=| 9-x2 |
当直线y=x+b过(3,0)时,可得b=-3;
当直线y=x+b与圆相切时,圆心(0,0)到直线的距离d=r=
| |b| | ||
|
解得:b=3
| 2 |
| 2 |
则P∩Q≠∅时b的取值范围是-3≤b≤3
| 2 |
故选C
点评:此题考查了直线与圆相交的性质,利用了数形结合的思想,熟练掌握数形结合思想是解本题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
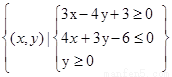 ,Q={(x,y)|(x-a)2+(y-b)2≤r2(r>0), 若“点M∈P”是“点M∈Q”的必要条件,则当r最大时ab的值是_____
,Q={(x,y)|(x-a)2+(y-b)2≤r2(r>0), 若“点M∈P”是“点M∈Q”的必要条件,则当r最大时ab的值是_____