题目内容

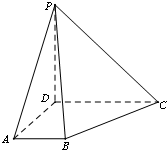
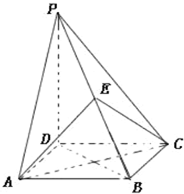
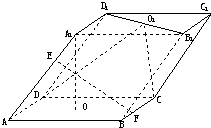
如图，A-BCDE是一个四棱锥，AB⊥平面BCDE，且四边形BCDE为矩形，则图中互相垂直的平面共有（　　）
A．4组B．5组C．6组D．7组

因为AB⊥平面BCDE，所以平面ABC⊥平面BCDE，平面ABD⊥平面BCDE，平面ABE⊥平面BCDE，
又因为四边形BCDE为矩形，所以BC⊥平面ABE⇒平面ABC⊥平面ABE，
同理可得平面ACD⊥平面ABC．平面ADE⊥平面ABE
故图中互相垂直的平面共有6组．
故选C．
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，PD⊥平面ABCD，AB∥CD，AD⊥DC，PD=AD=DC=2AB，则异面直线PA与BC所成角的余弦值为（　　）
A．
15
5
B．
10
5
C．-
10
5
D．
10
4
如图，直棱柱ABCD-A1B1C1D1中，底面ABCD是直角梯形，∠BAD=∠ADC=90°，AB=2AD=2CD=2．
（1）求证：AC⊥平面BB1C1C；
（2）在A1B1上是否存一点P，使得DP与平面BCB1与平面ACB1都平行？证明你的结论．
在长方形AA1B1B中，AB=2AA1，C，C1分别AB，A1B1是的中点（如图1）．将此长方形沿CC1对折，使平面AA1C1C⊥平面CC1B1B（如图2），已知D，E分别是A1B1，CC1的中点．
（1）求证：C1D∥平面A1BE；
（2）求证：平面A1BE⊥平面AA1B1B．
如图四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上，O为AC与BD的交点．
（1）求证：平面AEC⊥平面PDB；
（2）当E为PB中点时，求证：OE∥平面PDA，OE∥平面PDC．
（3）当PD=
2
AB且E为PB的中点时，求AE与平面PBC所成的角的大小．
如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
（1）求证：平面O1DC⊥平面ABCD；
（2）若点E、F分别在棱AA1、BC上，且AE=2EA1，问F在何处时，EF⊥AD？
四棱锥P-ABCD中，PC⊥平面ABCD，PC=2，在四边形ABCD中，∠B=∠C=90°，CD∥AB，AB=4，CD=1，点M在PB上，且MB=3PM，PB与平面ABC成30°角．
（1）求证：CM∥面PAD；
（2）求证：面PAB⊥面PAD；
（3）求点C到平面PAD的距离．
直三棱柱ABC-A1B1C1中，AC=BC=BB1=1，AB1=
3

（1）求证：平面AB1C⊥平面B1CB；
（2）求三棱锥A1-AB1C的体积．
在空间直角坐标系中，点P（-2，4，4）关于x轴和坐标原点的对称点分别为P1和P2，则|P1P2|=（　　）
A．4B．4
5
C．8D．8
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网