题目内容
关于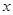 的不等式
的不等式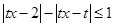 ,其中
,其中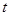 是实参数.
是实参数.
(1)当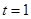 时,解上面的不等式.
时,解上面的不等式.
(2)若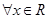 ,上面的不等式均成立,求实数
,上面的不等式均成立,求实数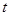 的范围.
的范围.
(1)R,(2)
解析试题分析:(1)t=1时,原不等式化为|x-2|-|x-1| 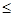 1,由绝对值的几何意义知,
1,由绝对值的几何意义知, .
.
(2)由绝对值不等式的性质 ,即
,即 恒成立,解得
恒成立,解得 ,所以实数
,所以实数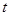 的范围
的范围 。
。
考点:本题主要考查简单绝对值不等式的解法。
点评:简单题,解简单绝对值不等式,一般要考虑去绝对值的符号。有时利用绝对值的几何意义则更为简单。

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
下列各式中,最小值等于2的是( )
A. | B. | C. | D. |
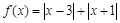 .
.
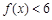 成立的
成立的 的取值范围;
的取值范围;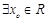 ,
,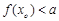 ,求实数
,求实数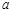 的取值范围.
的取值范围. .
. 的解集为
的解集为 时, 求实数
时, 求实数 的值;
的值; ,
,  恒成立, 求实数
恒成立, 求实数 的取值范围.
的取值范围.  +4m-5)x
+4m-5)x
 且
且 ,求
,求 的最小值.
的最小值.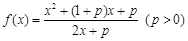
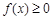 ;
;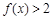 对
对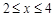 时恒成立,求p的范围.
时恒成立,求p的范围.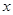 的不等式
的不等式 .
. 时,求不等式的解集;
时,求不等式的解集; 时,解不等式.
时,解不等式.