题目内容
(理科)已知二次函数f(x)=x2+ax+b(a,b∈R)的定义域为[-1,1],且|f(x)|的最大值为M.
(Ⅰ)试证明|1+b|≤M;
(Ⅱ)试证明M≥
;
(Ⅲ)当M=
时,试求出f(x)的解析式.
(Ⅰ)试证明|1+b|≤M;
(Ⅱ)试证明M≥
| 1 |
| 2 |
(Ⅲ)当M=
| 1 |
| 2 |
(Ⅰ)证明:∵M≥|f(-1)|=|1-a+b|,M≥|f(1)|=|1+a+b|
∴2M≥|1-a+b|+|1+a+b|≥|(1-a+b)+(1+a+b)|=2|1+b|
∴M≥|1+b|
(Ⅱ)证明:依题意,M≥|f(-1)|,M≥|f(0)|,M≥|f(1)|
又|f(-1)|=|1-a+b|,|f(1)|=|1+a+b|,|f(0)|=|b|
∴4M≥|f(-1)|+|f(0)|+|f(1)|=|1-a+b|+2|b|+|1+a+b|≥|(1-a+b)-2b+(1+a+b)|=2
∴M≥
(Ⅲ)依M=
时,|f(0)|=|b|≤
,-
≤b≤
①同理-
≤1+a+b≤
②-
≤1-a+b≤
③
②+③得:-
≤b≤-
④由①、④得:b=-
.
当b=-
时,分别代入②、③得:
?a=0,因此f(x)=x2-
.
∴2M≥|1-a+b|+|1+a+b|≥|(1-a+b)+(1+a+b)|=2|1+b|
∴M≥|1+b|
(Ⅱ)证明:依题意,M≥|f(-1)|,M≥|f(0)|,M≥|f(1)|
又|f(-1)|=|1-a+b|,|f(1)|=|1+a+b|,|f(0)|=|b|
∴4M≥|f(-1)|+|f(0)|+|f(1)|=|1-a+b|+2|b|+|1+a+b|≥|(1-a+b)-2b+(1+a+b)|=2
∴M≥
| 1 |
| 2 |
(Ⅲ)依M=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②+③得:-
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当b=-
| 1 |
| 2 |
|
| 1 |
| 2 |

练习册系列答案
相关题目
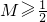 ;
;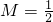 时,试求出f(x)的解析式.
时,试求出f(x)的解析式. ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn; ,求数列{cn}的变号数.
,求数列{cn}的变号数. ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn; ,求数列{cn}的变号数.
,求数列{cn}的变号数.