题目内容
已知f(x)是定义在R上的奇函数,且f(x+2)+f(x)=0,当x∈[0,1]时,f(x)=2x-1,则 的值为
的值为
- A.

- B.
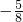
- C.

- D.

A
分析:通过函数f(x)的奇偶性及f(x+2)+f(x)=0求得 =f(log2
=f(log2 )再根据f(x)在[0,1]上的解析式得到答案.
)再根据f(x)在[0,1]上的解析式得到答案.
解答:∵函数f(x)为奇函数
∴ =-f(log26)
=-f(log26)
又∵f(x+2)+f(x)=0,即-f(x)=f(x+2)
∴-f(x)=f(x-2)
∴-f(log26)=f(log26-2)=f(log2 )
)
∵0<log2<1
∴f(log2 )=
)= =
=
故选A
点评:本题主要考查了函数的周期性.由于函数在不同区间的解析式不同,故要特别留意x的范围.
分析:通过函数f(x)的奇偶性及f(x+2)+f(x)=0求得
 =f(log2
=f(log2 )再根据f(x)在[0,1]上的解析式得到答案.
)再根据f(x)在[0,1]上的解析式得到答案.解答:∵函数f(x)为奇函数
∴
 =-f(log26)
=-f(log26)又∵f(x+2)+f(x)=0,即-f(x)=f(x+2)
∴-f(x)=f(x-2)
∴-f(log26)=f(log26-2)=f(log2
 )
)∵0<log2<1
∴f(log2
 )=
)= =
=
故选A
点评:本题主要考查了函数的周期性.由于函数在不同区间的解析式不同,故要特别留意x的范围.

练习册系列答案
相关题目