题目内容
过双曲线M:x2-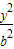 =1的左顶点A作斜率为2的直线l,若l与双曲线M的两条渐近线分别相交于点B、C,且
=1的左顶点A作斜率为2的直线l,若l与双曲线M的两条渐近线分别相交于点B、C,且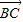 =2
=2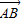 ,则双曲线M的离心率是( )
,则双曲线M的离心率是( )A.
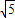
B.
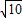
C.
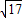
D.
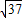
【答案】分析:根据双曲线方程,得渐近线方程为y=-bx或y=bx.设直线l的方程为y=2x+1,与渐近线方程联解分别得到B、C的纵坐标关于b的式子.由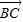 =2
=2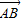 ,得3yB=yC,利用向量坐标公式建立关于b的方程并解之可得,由此算出c,即可得到该双曲线的离心率.
,得3yB=yC,利用向量坐标公式建立关于b的方程并解之可得,由此算出c,即可得到该双曲线的离心率.
解答:解:由题可知A(-1,0)所以直线l的方程为y=2x+1
∵双曲线M的方程为x2-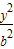 =1,∴两条渐近线方程为y=-bx或y=bx
=1,∴两条渐近线方程为y=-bx或y=bx
由y=2x+1和y=-bx联解,得B的纵坐标为yB=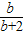 ,同理可得C的横坐标为xC=
,同理可得C的横坐标为xC=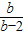
∵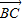 =2
=2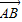 ,可得3yB=yC,
,可得3yB=yC,
即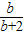 •3=
•3=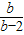 ,解之得b=4,(b=0舍去)
,解之得b=4,(b=0舍去)
因此,c=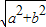 =
=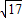 ,可得双曲线的离心率e=
,可得双曲线的离心率e=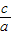 =
=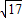 .
.
故选C.
点评:本题给出双曲线的渐近线与过左顶点A的直线相交于B、C两点,求双曲线的离心率.着重考查了双曲线的标准方程和简单几何性质等知识,属于中档题.
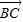 =2
=2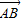 ,得3yB=yC,利用向量坐标公式建立关于b的方程并解之可得,由此算出c,即可得到该双曲线的离心率.
,得3yB=yC,利用向量坐标公式建立关于b的方程并解之可得,由此算出c,即可得到该双曲线的离心率.解答:解:由题可知A(-1,0)所以直线l的方程为y=2x+1
∵双曲线M的方程为x2-
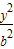 =1,∴两条渐近线方程为y=-bx或y=bx
=1,∴两条渐近线方程为y=-bx或y=bx由y=2x+1和y=-bx联解,得B的纵坐标为yB=
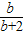 ,同理可得C的横坐标为xC=
,同理可得C的横坐标为xC=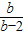
∵
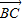 =2
=2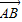 ,可得3yB=yC,
,可得3yB=yC,即
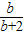 •3=
•3=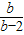 ,解之得b=4,(b=0舍去)
,解之得b=4,(b=0舍去)因此,c=
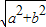 =
=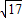 ,可得双曲线的离心率e=
,可得双曲线的离心率e=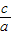 =
=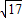 .
.故选C.
点评:本题给出双曲线的渐近线与过左顶点A的直线相交于B、C两点,求双曲线的离心率.着重考查了双曲线的标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
相关题目