题目内容
【题目】已知⊙O:x2+y2=1和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程.
【答案】
(1)解:连接OQ,∵切点为Q,PQ⊥OQ,由勾股定理可得 PQ2=OP2﹣OQ2.
由已知PQ=PA,可得 PQ2=PA2,即 (a2+b2)﹣1=(a﹣2)2+(b﹣1)2.
化简可得 2a+b﹣3=0
(2)解:
∵PQ= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
故当a= ![]() 时,线段PQ取得最小值为
时,线段PQ取得最小值为 ![]()
(3)解:若以P为圆心所作的⊙P 的半径为R,由于⊙O的半径为1,∴|R﹣1|≤PO≤R+1.
而OP= ![]() =
= ![]() =
= ![]() ,故当a=
,故当a= ![]() 时,PO取得最小值为
时,PO取得最小值为 ![]() ,
,
此时,b=﹣2a+3= ![]() ,R取得最小值为
,R取得最小值为 ![]() ﹣1.
﹣1.
故半径最小时⊙P 的方程为 ![]() +
+ ![]() =
= ![]()
【解析】(1)由勾股定理可得 PQ2=OP2﹣OQ2=PA2 , 即 (a2+b2)﹣1=(a﹣2)2+(b﹣1)2 , 化简可得a,b间满足的等量关系.(2)由于 PQ= ![]() =
= ![]() ,利用二次函数的性质求出它的最小值.(3)设⊙P 的半径为R,可得|R﹣1|≤PO≤R+1.利用二次函数的性质求得OP=
,利用二次函数的性质求出它的最小值.(3)设⊙P 的半径为R,可得|R﹣1|≤PO≤R+1.利用二次函数的性质求得OP= ![]() 的最小值为
的最小值为 ![]() ,此时,求得b=﹣2a+3=
,此时,求得b=﹣2a+3= ![]() ,R取得最小值为
,R取得最小值为 ![]() ﹣1,从而得到圆的标准方程.
﹣1,从而得到圆的标准方程.

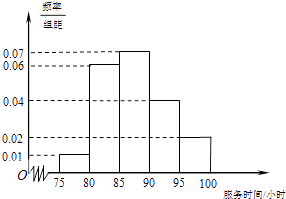
【题目】2016年高一新生入学后,为了了解新生学业水平,某区对新生进行了水平测试,随机抽取了50名新生的成绩,其相关数据统计如下:
分数段 | 频数 | 选择题得分24分以上(含24分) |
| 5 | 2 |
| 10 | 4 |
| 15 | 12 |
| 10 | 6 |
| 5 | 4 |
| 5 | 5 |
(Ⅰ)若从分数在![]() ,
, ![]() 的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
(Ⅱ)在(Ⅰ)的条件下,记选中的4名新生中选择题得分不足24分的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.