题目内容
已知
 。
。
(1)若 ,
, 时,求证:
时,求证: 对于
对于 恒成立;
恒成立;
(2)若 ,且
,且 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;
(3)利用(1)的结论证明:若 ,则
,则 。
。
解:(1)设 ,
,
则
|
| (-1,0) | 0 | (0,+ |
|
| + | 0 | - |
|
| ↗ | 最大值 | ↘ |
 当
当 时,
时, 有最大值0
有最大值0 
 恒成立。
恒成立。
即 对于
对于 恒成立。
恒成立。
(2) 时
时 ,
,
 有单调递减区间,
有单调递减区间,
 有解,即
有解,即 有解,
有解,

 有解,
有解,
① 时合题意
时合题意
② 时,
时, ,即
,即 ,
,

 的取值范围是
的取值范围是
(3)证明:

当 时,
时, ,由(1)知
,由(1)知

等号在 即
即 时成立。
时成立。
而 , 所以
, 所以 成立。
成立。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 )
)

 ,则x+y的最小值是___________
,则x+y的最小值是___________ 是等差数列,首项
是等差数列,首项 ,
, ,则使前
,则使前 项和
项和  成立的最大自然数
成立的最大自然数 …
… 。
。 ;
; 的值;
的值; 的值。
的值。 是 ( )
是 ( )  满足不等式组
满足不等式组 ,则
,则 的最小值为 。
的最小值为 。 ,(其中
,(其中 表示
表示 的夹角),则对于两个平面向量
的夹角),则对于两个平面向量 ,下列结论不一定成立的是( )
,下列结论不一定成立的是( ) B.
B.
 D.若
D.若 ,则
,则 平行
平行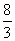 cm3 B、8cm3
cm3 B、8cm3 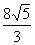 cm3
cm3