Question

已知二次函数f（x）=x²+ax+m+1，关于x的不等式f（x）＜（2m-1）x+1-m²的解集为（m，m+1），其中m为非零常数．设．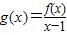
（1）求a的值；
（2）k（k∈R）如何取值时，函数φ（x）=g（x）-kln（x-1）存在极值点，并求出极值点．

Answer 1

【答案】分析：（1）利用一元二次不等式的解集即可得出；
（2）在定义域内分类讨论△与方程的实数根的情况即可得出．
解答：解：（1）∵关于x的不等式f（x）＜（2m-1）x+1-m²的解集为（m，m+1），
即不等式x²+（a+1-2m）x+m²+m＜0的解集为（m，m+1），
∴x²+（a+1-2m）x+m²+m=（x-m）（x-m-1）．
∴x²+（a+1-2m）x+m²+m=x²-（2m+1）x+m（m+1）．
∴a+1-2m=-（2m+1）．
∴a=-2．
（2）由（1）得=．
∴φ（x）=g（x）-kln（x-1）=-kln（x-1）的定义域为（1，+∞）．
∴φ'（x）=1-=．
方程x²-（2+k）x+k-m+1=0（*）的判别式△=（2+k）²-4（k-m+1）=k²+4m．
①当m＞0时，△＞0，
方程（*）的两个实根为，，
则x∈（1，x₂）时，φ'（x）＜0；x∈（x₂，+∞）时，φ'（x）＞0．
∴函数φ（x）在（1，x₂）上单调递减，在（x₂，+∞）上单调递增．
∴函数φ（x）有极小值点x₂．
②当m＜0时，由△＞0，得或，
若，则，，
故x∈（1，+∞）时，φ'（x）＞0，
∴函数φ（x）在（1，+∞）上单调递增．
∴函数φ（x）没有极值点．
若时，，，
则x∈（1，x₁）时，φ'（x）＞0；x∈（x₁，x₂）时，φ'（x）＜0；x∈（x₂，+∞）时，φ'（x）＞0．
∴函数φ（x）在（1，x₁）上单调递增，在（x₁，x₂）上单调递减，在（x₂，+∞）上单调递增．
∴函数φ（x）有极小值点x₂，有极大值点x₁．
综上所述，当m＞0时，k取任意实数，函数φ（x）有极小值点x₂；
当m＜0时，，函数φ（x）有极小值点x₂，有极大值点x₁．
（其中，）．
点评：熟练掌握一元二次不等式的解法、分类讨论的思想方法、△与方程的实数根的情况、利用导数研究函数的单调性与极值等方法是解题的关键．