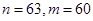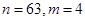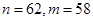题目内容
公差不为零的等差数列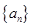 的前
的前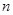 项和为
项和为 ,若
,若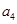 是
是 与
与 的等比中项,且
的等比中项,且 ,则
,则 =( )
=( )
| A.80 | B.160 | C.320 | D.640 |
C
解析试题分析:公差不为零的等差数列{an}中,由a4是a3与a7的等比中项,S10=60,利用等差数列的通项公式和前n项和公式列方程组解得首项与公差,由此能求出S20. 解:∵a4是a3与a7的等比中项,S10=60,(a1+3d)2=(a1+2d)(a1+6d)∴10a1+45 d=60,∵公差不为零,∴解得a1=-3,d=2,∴S20=20a1+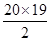 d=20×(-3)+190×2=320.故选C.
d=20×(-3)+190×2=320.故选C.
考点:等差数列的前n项和的公式
点评:本题考查学生灵活运用等差数列的前n项和的公式及等比数列的通项公式化简求值,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=xa的图象过点(4,2),令an=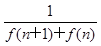 ,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
A.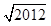 -1 -1 | B. -1 -1 | C.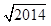 -1 -1 | D.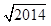 +1 +1 |
已知数列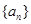 的前n项和
的前n项和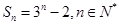 ,则( )
,则( )
A.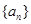 是递增的等比数列 是递增的等比数列 | B.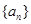 是递增数列,但不是等比数列 是递增数列,但不是等比数列 |
C.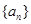 是递减的等比数列 是递减的等比数列 | D.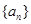 不是等比数列,也不单调 不是等比数列,也不单调 |
数列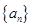 的通项公式是
的通项公式是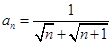 ,若前n项和为10,则项数
,若前n项和为10,则项数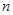 为( )
为( )
| A.11 | B.99 | C.120 | D.121 |
已知数列{an}的前n项和Sn=n2-9n,第k项满足5<ak<8,则k=( ).
| A.9 | B.8 | C.7 | D.6 |
已知数列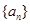 的前n项和
的前n项和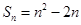
 ,则
,则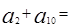 ( )
( )
| A.20 | B.19 | C.18 | D.17 |
已知函数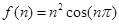 ,且
,且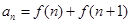 ,则
,则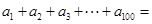 ( )
( )
| A.0 | B.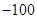 | C.100 | D.10200 |
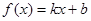 的图像经过点
的图像经过点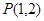 和
和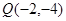 ,令
,令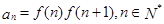 ,记数列
,记数列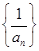 的前项和为
的前项和为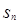 ,当
,当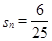 时,
时, 的值等于( )
的值等于( )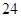
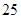
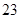
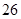
 表示位于从上到下第
表示位于从上到下第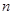 行,从左到右
行,从左到右 列的数 ,比如
列的数 ,比如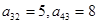 ,若
,若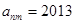 ,则有( )
,则有( )