题目内容
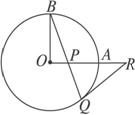
如图(1)现将PA向上平移至图
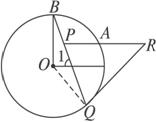
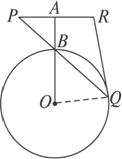
(2)若将PA向上平移至⊙O外,结论还成立吗?如图
(1) (2) (3)
图
解析:(1)成立.
证明:连结OQ,则QR⊥OQ.
∴∠PQR+∠BQO=90°.
∵∠RPQ=∠1,∠1+∠B=90°,
∴∠RPQ+∠B=90°.
又OB=OQ,∴∠B=∠BQO.
∴∠PQR=∠RPQ.∴RP=RQ.
(2)结论仍然成立.
证明:连结OQ,则OQ⊥RQ.
∴∠RQO=90°.
∴∠RQP+∠BQO=90°.
∵OA⊥PA,∴∠P+∠ABP=90°.
又∠PBA=∠OBQ,∵OB=OQ,
∴∠OBQ=∠OQB.
∴∠P=∠PQR.∴RP=RQ.

练习册系列答案
相关题目
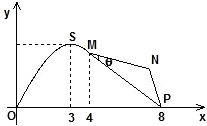 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为 如图,
如图,