题目内容
数列 记
记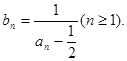
(1)求b1、b2、b3、b4的值;
(2)求数列 的通项公式及数列
的通项公式及数列 的前n项和
的前n项和
(1)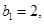
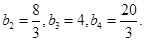 (2)
(2)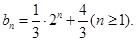
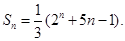
解析试题分析:(1)利用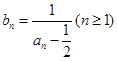 先将数列
先将数列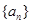 的递推关系
的递推关系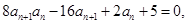 转化为数列
转化为数列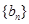 的递推关系
的递推关系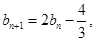 ,再由
,再由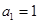 求出
求出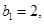 代入
代入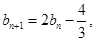 可求出
可求出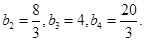 (2)对数列
(2)对数列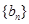 的递推关系
的递推关系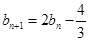 进行变形
进行变形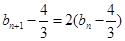 ,构造出新数列
,构造出新数列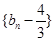 ,利用新数列
,利用新数列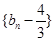 成等比,求出
成等比,求出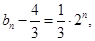 即
即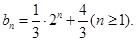 又
又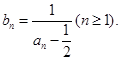 因此可求出数列
因此可求出数列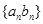 的通项公式
的通项公式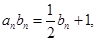 ,这是一个等比数列与常数列的和,因此利用分组求和法求出前n项和
,这是一个等比数列与常数列的和,因此利用分组求和法求出前n项和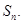
试题解析:解(1)由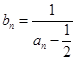 得
得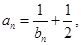 代人递推关系
代人递推关系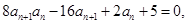
整理得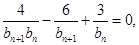 即
即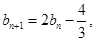 由
由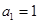 有
有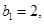 所以
所以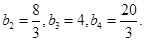 6分
6分
(2)由
所以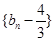 是首项为
是首项为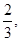 公比
公比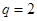 的等比数列,故
的等比数列,故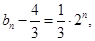 即
即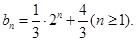
由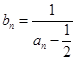 得
得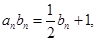
故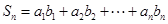
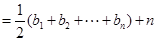

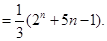 ..12分
..12分
考点:数列通项,前n项和

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (n∈N*),求设数列{bn}的前n项和Tn.
(n∈N*),求设数列{bn}的前n项和Tn. bn=1.
bn=1.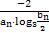 ,{cn}的前n项和为Tn,若Tn<
,{cn}的前n项和为Tn,若Tn<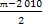 对一切n∈N*都成立,求最小正整数m.
对一切n∈N*都成立,求最小正整数m.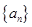 的前
的前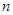 项和为
项和为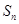 ,
,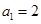 ,
,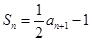
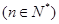 .
.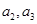 ;
;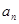 ;
;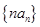 的前
的前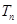 .
.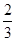 an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.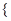 an
an 为等比数列,它的前n项和为Sn,a1=1,且
为等比数列,它的前n项和为Sn,a1=1,且 .
. 的通项公式;
的通项公式;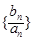 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前n项和Tn.
的前n项和Tn. 中,
中,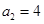 ;
;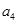 是
是 与
与 的等比中项.
的等比中项.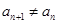 .求数列
.求数列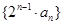 的前
的前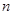 项和.
项和.