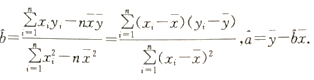Question

【题目】定义首项为1且公比为正数的等比数列为“M－数列”.

（1）已知等比数列{an}满足：，求证:数列{an}为“M－数列”；

（2）已知数列{bn}满足:，其中Sn为数列{bn}的前n项和．

①求数列{bn}的通项公式；

②设m为正整数，若存在“M－数列”{cn}，对任意正整数k，当k≤m时，都有成立，求m的最大值．

Answer 1

【答案】（1）见解析；

（2）①bn=n；②5.

【解析】

（1）由题意分别求得数列的首项和公比即可证得题中的结论；

（2）①由题意利用递推关系式讨论可得数列{bn}是等差数列，据此即可确定其通项公式；

②由①确定的值，将原问题进行等价转化，构造函数，结合导函数研究函数的性质即可求得m的最大值．

（1）设等比数列{an}的公比为q，所以a1≠0，q≠0.

由，得，解得．

因此数列为“M—数列”.

（2）①因为，所以．

由得，则.

由，得，

当时，由，得，

整理得．

所以数列{bn}是首项和公差均为1的等差数列.

因此，数列{bn}的通项公式为bn=n.

②由①知，bk=k，.

因为数列{cn}为“M–数列”，设公比为q，所以c1=1，q>0.

因为ck≤bk≤ck+1，所以，其中k=1，2，3，…，m.

当k=1时，有q≥1；

当k=2，3，…，m时，有．

设f（x）=，则．

令，得x=e.列表如下：

x		e	(e，+∞)
	+	0	–
f（x）		极大值

因为，所以．

取，当k=1，2，3，4，5时，，即，

经检验知也成立．

因此所求m的最大值不小于5．

若m≥6，分别取k=3，6，得3≤q3，且q5≤6，从而q15≥243，且q15≤216，

所以q不存在.因此所求m的最大值小于6.

综上，所求m的最大值为5．