��Ŀ����
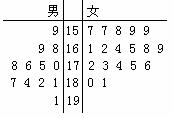
����С������12�֣���26�������ѧ���ļ��˶��Ὣ��2011��8��12�յ�23�������ھ��� ��Ϊ�˸�ýӴ���������ί����ijѧԺ��ļ��12����־Ը�ߺ�18��Ů־Ը�ߡ�����30��־Ը�ߵ����߱��������ʾ�ľ�Ҷͼ����λ��cm���� ��������175cm���ϣ�����175cm������Ϊ���߸��ӡ��� ������175cm���£�������175cm������Ϊ���Ǹ߸��ӡ�����ֻ�С�Ů�߸��ӡ��ŵ��Ρ�����С�㡱��
 |
��1������÷ֲ�����ķ����ӡ��߸��ӡ��͡��Ǹ߸�![]() �ӡ�������ȡ5�ˣ��ٴ���5����ѡ2�ˣ���ô������һ���Ǹ߸��ӡ��ĸ����Ƕ��٣�
�ӡ�������ȡ5�ˣ��ٴ���5����ѡ2�ˣ���ô������һ���Ǹ߸��ӡ��ĸ����Ƕ��٣�
��2���������С��߸��ӡ���ѡ3��־Ը�ߣ���![]() ��ʾ��ѡ־Ը�����ܵ��Ρ�����С�㡱����������д��
��ʾ��ѡ־Ը�����ܵ��Ρ�����С�㡱����������д��![]() �ķֲ��У�����
�ķֲ��У�����![]() ����ѧ������
����ѧ������
�⣺��1�����ݾ�Ҷͼ���С��߸��ӡ�12�ˣ����Ǹ߸��ӡ�18�ˣ���������������������1��
�÷ֲ�����ķ�����ÿ���˱����еĸ�����![]() �� ��������������������2��
�� ��������������������2��
����ѡ�еġ��߸��ӡ���![]() �ˣ����Ǹ�
�ˣ����Ǹ�![]() ���ӡ���
���ӡ���![]() �ˣ���������������3��
�ˣ���������������3��
���¼�![]() ��ʾ��������һ�����߸��ӡ���ѡ�С��������Ķ����¼�
��ʾ��������һ�����߸��ӡ���ѡ�С��������Ķ����¼�![]() ��ʾ��û��һ�����߸��ӡ���ѡ�С���
��ʾ��û��һ�����߸��ӡ���ѡ�С���
����![]()
![]()
![]()
![]() �� ������������������������5��
�� ������������������������5��
��ˣ�������һ���ǡ��߸��ӡ��ĸ�����![]() �� ����������������������6��
�� ����������������������6��
��![]() ���������⣬
���������⣬![]() ��ȡֵΪ
��ȡֵΪ![]() ��������������������������������������������7��
��������������������������������������������7��
��![]() ��������
��������![]() ��
��
��![]() ��
�� ![]() �� ��������������������9��
�� ��������������������9��
����ˣ�![]() �ķֲ������£�
�ķֲ������£�
|
|
|
|
|
|
|
|
|
|
|
|
������������10��
![]() �� ��������������������12��
�� ��������������������12��
��˵����������Ҫ���쾥Ҷͼ���ֲ����������¼��ĸ��ʡ������¼��ĸ��ʡ���������ķֲ����Լ���ѧ�����Ȼ���֪ʶ���������ø���ͳ��֪ʶ�����ʵ����������������ݴ���������Ӧ����ʶ��

 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д� �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�