题目内容
给定函数
(1)试求函数f(x)的单调减区间;
(2)已知各项均为负的数列{an}满足,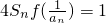 ,求证:-
,求证:- <
< <-
<- ;
;
(3)设bn=- ,Tn为数列 {bn} 的前n项和,求证:T2012-1<ln2012<T2011.
,Tn为数列 {bn} 的前n项和,求证:T2012-1<ln2012<T2011.
解:(1) 的定义域为{x|x≠1}
的定义域为{x|x≠1}
f′(x)=
由f′(x)<0得0<x<1或1<x<2
单调减区间为(0,1)和(1,2)
(2)由已知可得2 ,当n≥2时,2
,当n≥2时,2
两式相减得(an+an-1)(an-an-1+1)=0
∴an=-an-1或an-an-1=-1
当n=1时,2a1=a1-a12得a1=-1,若an=-an-1,则a2=1这与题设矛盾
∴an-an-1=-1
∴an=-n
于是,待证不等式即为 .
.
为此,我们考虑证明不等式
令1+ =t.则t>1,x=
=t.则t>1,x=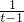
再令g(t)=t-1-lnt,g′(t)=1-
由t∈(1,+∞)知g′(t)>0
∴当t∈(1,+∞)时,g(t)单调递增∴g(t)>g(1)=0 于是t-1>lnt
即 ,x>0 ①
,x>0 ①
令h(t)=lnt-1+ ,h′(t)=
,h′(t)= 由t∈(1,+∞)知h′(t)>0
由t∈(1,+∞)知h′(t)>0
∴当t∈(1,+∞)时,h(t)单调递增∴h(t)>h(1)=0 于是lnt>1-
即 ,x>0 ②
,x>0 ②
由①、②可知 ,x>0
,x>0
所以, ,即
,即 
(3)由(2)可知 则
则 
在 中令n=1,2,3…..2010,2011并将各式相加得
中令n=1,2,3…..2010,2011并将各式相加得
即 T2012-1<ln2012<T2011…14
分析:(1)先写出 的定义域,再求其导数,由f′(x)<0解出单调减区间即可;
的定义域,再求其导数,由f′(x)<0解出单调减区间即可;
(2)由已知可得2 ,再由此式得到2
,再由此式得到2 ,两式相减得结合已知条件得出an的通项公式,于是,待证不等式即为
,两式相减得结合已知条件得出an的通项公式,于是,待证不等式即为 .为此,我们考虑证明不等式
.为此,我们考虑证明不等式 ,下面利用换元法结合导数工具进行证明.
,下面利用换元法结合导数工具进行证明.
(3)由(2)可知 则
则  ,下面只须在
,下面只须在 中令n=1,2,3…..2010,2011并将各式相加即可.
中令n=1,2,3…..2010,2011并将各式相加即可.
点评:本题考查数列和不等式的综合,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
 的定义域为{x|x≠1}
的定义域为{x|x≠1}f′(x)=

由f′(x)<0得0<x<1或1<x<2
单调减区间为(0,1)和(1,2)
(2)由已知可得2
 ,当n≥2时,2
,当n≥2时,2
两式相减得(an+an-1)(an-an-1+1)=0
∴an=-an-1或an-an-1=-1
当n=1时,2a1=a1-a12得a1=-1,若an=-an-1,则a2=1这与题设矛盾
∴an-an-1=-1
∴an=-n
于是,待证不等式即为
 .
.为此,我们考虑证明不等式

令1+
 =t.则t>1,x=
=t.则t>1,x=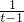
再令g(t)=t-1-lnt,g′(t)=1-

由t∈(1,+∞)知g′(t)>0
∴当t∈(1,+∞)时,g(t)单调递增∴g(t)>g(1)=0 于是t-1>lnt
即
 ,x>0 ①
,x>0 ①令h(t)=lnt-1+
 ,h′(t)=
,h′(t)= 由t∈(1,+∞)知h′(t)>0
由t∈(1,+∞)知h′(t)>0∴当t∈(1,+∞)时,h(t)单调递增∴h(t)>h(1)=0 于是lnt>1-

即
 ,x>0 ②
,x>0 ②由①、②可知
 ,x>0
,x>0 所以,
 ,即
,即 
(3)由(2)可知
 则
则 
在
 中令n=1,2,3…..2010,2011并将各式相加得
中令n=1,2,3…..2010,2011并将各式相加得
即 T2012-1<ln2012<T2011…14
分析:(1)先写出
 的定义域,再求其导数,由f′(x)<0解出单调减区间即可;
的定义域,再求其导数,由f′(x)<0解出单调减区间即可;(2)由已知可得2
 ,再由此式得到2
,再由此式得到2 ,两式相减得结合已知条件得出an的通项公式,于是,待证不等式即为
,两式相减得结合已知条件得出an的通项公式,于是,待证不等式即为 .为此,我们考虑证明不等式
.为此,我们考虑证明不等式 ,下面利用换元法结合导数工具进行证明.
,下面利用换元法结合导数工具进行证明.(3)由(2)可知
 则
则  ,下面只须在
,下面只须在 中令n=1,2,3…..2010,2011并将各式相加即可.
中令n=1,2,3…..2010,2011并将各式相加即可.点评:本题考查数列和不等式的综合,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 (2012•卢湾区一模)已知函数f(x)=
(2012•卢湾区一模)已知函数f(x)= (2012•卢湾区一模)已知函数f(x)=
(2012•卢湾区一模)已知函数f(x)= )<
)< ,则称f(x)为定义在D上的C函数.
,则称f(x)为定义在D上的C函数.