Question

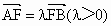(2006全国Ⅱ，21)已知抛物线的焦点为F，A、B是抛物线上的两动点，且．过A、B两点分别作抛物线的切线，设其交点为M．

(1)证明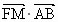：为定值；

(2)设△ABM的面积为S，写出S=f(λ)的表达式，并求S的最小值．

Answer 1

答案：略
解析：

解析：(1)由已知条件，得F(0，1)，λ＞0． 设，．由， 即得， 将①式两边平方并把， 代入得，　　　　　　③ 解②、③式得，，且有． 抛物线方程为．求导得． 所以过抛物线上A、B两点的切线方程分别是， ，即，． 解出两条切线的交点M的坐标为． 所以， ， 所以为定值，其值为0． (2)由(1)知在△ABM中，FM⊥AB，因而． ． 因为|AF|、|BF|分别等于A、B到抛物线准线y=－1的距离，所以 ． 于是， 由，知S≥4， 且当λ=1时，S取得最小值4．