题目内容
从8名男生7名女生中选出4人分别参加4个不同的课外活动小组,在选出的4人中至少有2男1女的选法有多少种?
错解:先从8名男生中选取2人,有![]() 种选法;再从7名女生中选取1人,有
种选法;再从7名女生中选取1人,有![]() 种选法;最后从余下的男、女生(共12人)中选出1人,有
种选法;最后从余下的男、女生(共12人)中选出1人,有![]() 种选法.然后,将选出的4人分别分配到四个不同的课外活动小组,所以,符合题意的选法共有(
种选法.然后,将选出的4人分别分配到四个不同的课外活动小组,所以,符合题意的选法共有(![]()
![]()
![]() )
)![]() =56 448种不同的选法.
=56 448种不同的选法.
分析:错解在于选元时有重复.把8名男生记为①,②,③,④,⑤,⑥,⑦,⑧,7名女生记为a,b,c,d,e,f,g.那么,比如对于任何一种一女三男的选法,假如选“a,①,②,③”都重复计算了三次:(1)先选a,再选①,②,最后选③;(2)先选a,再选①,③最后选②;(3)先选a,再选②,③,最后选①.同理,在选出的2女2男的每一种选法,在原解法中都被重复计算了二次.
因此,正确的解法是:依题意分两步完成,第一步先选出符合条件的4人,第二步是选出的4人分别参加4个不同的课外活动小组,而第一步中又分两类:第一类是选出1女3男有![]()
![]() 种;第二类是选出2女2男有
种;第二类是选出2女2男有![]()
![]() 种,故符合条件的选法有
种,故符合条件的选法有
(![]()
![]() +
+![]()
![]() )
)![]() =23 520(种).
=23 520(种).

从某学校高三年级 名学生中随机抽取
名学生中随机抽取 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 .第二组
.第二组 ; 第八组
; 第八组 ,下图是按上述分组方法得到的条形图.
,下图是按上述分组方法得到的条形图.

(1)根据已知条件填写下面表格:
|
组 别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
样本数 |
|
|
|
|
|
|
|
|
(2)估计这所学校高三年级 名学生中身高在
名学生中身高在 以上(含
以上(含 )的人数;
)的人数;
(3)在样本中,若第二组有 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
(本小题满分14分)
从某学校高一年级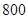 名学生中随机抽取
名学生中随机抽取 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 .第二组
.第二组 ;…第八组
;…第八组 ,右图
,右图
是按上述分组方法得到的条形图.
(1)根据已知条件填写下面表格:
|
组 别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
样本数 |
|
|
|
|
|
|
|
|
(2)估计这所学校高一年级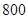 名学生中身高在
名学生中身高在 以上(含
以上(含 )的人数;
)的人数;
(3)在样本中,若第二组有 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
从某学校高三年级![]() 名学生中随机抽取
名学生中随机抽取![]() 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于![]()
和![]() 之间,将测量结果按如下方式分成
之间,将测量结果按如下方式分成

八组:第一组![]() .第二组
.第二组![]() ;…第八组
;…第八组![]() ,上图是按上述分组方法得到的条形图. (1)根据已知条件填写下面表格:
,上图是按上述分组方法得到的条形图. (1)根据已知条件填写下面表格:
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 样本数 | 2 | 4 | 10 | 10 | 15 | 4 |
(2)估计这所学校高三年级![]() 名学生中身高在
名学生中身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(3)在样本中,若第二组有![]() 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有![]() 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
 从某学校高三年级
从某学校高三年级
 名学生中随机抽取
名学生中随机抽取 名测量身高,据
名测量身高,据
测量被抽取的学生的身高全部介于
和 之间,将测量结果按如下方式分成
之间,将测量结果按如下方式分成
八组:第一组 .第二组
.第二组 ;…第八组
;…第八组 ,右图是按上述分组方法得到的条形图. (1)根据已知条件填写下面表格:
,右图是按上述分组方法得到的条形图. (1)根据已知条件填写下面表格:
|
组别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
样本数 |
|
|
|
|
|
|
|
|
(2)估计这所学校高三年级 名学生中身高在
名学生中身高在 以上(含
以上(含 )的人数;
)的人数;
(3)在样本中,若第二组有 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?