题目内容
三棱锥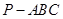 的高为
的高为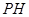 ,若三个侧面两两垂直,则
,若三个侧面两两垂直,则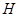 一定为△
一定为△ 的( )
的( )
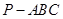 的高为
的高为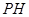 ,若三个侧面两两垂直,则
,若三个侧面两两垂直,则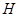 一定为△
一定为△ 的( )
的( )| A.垂心 | B.外心 | C.内心 | D.重心 |
A
试题分析:因为三个侧面两两垂直,所以
 。连结AH并延长交BC于点D。由
。连结AH并延长交BC于点D。由 知,
知, ①,由
①,由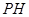 是三棱锥
是三棱锥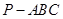 的高得,
的高得, ②。由①②得,
②。由①②得, 。同理:连结BH并延长交AC于点E、连结CH并延长交AB于点F,则
。同理:连结BH并延长交AC于点E、连结CH并延长交AB于点F,则 ,
, 。所以,点H是三角形三边上高的交点,即H是三角形的垂心。
。所以,点H是三角形三边上高的交点,即H是三角形的垂心。点评:本题需要掌握好三角形的各种“心”。

练习册系列答案
相关题目
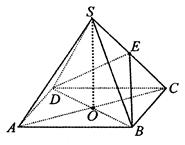
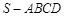 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形,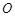 是
是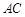 与
与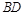 的交点,
的交点,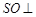 平面
平面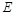 是侧棱
是侧棱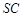 的中点,异面直线
的中点,异面直线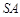 和
和 所成角的大小是60
所成角的大小是60 .
.
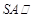 平面
平面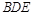 ;
;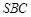 所成角的正弦值.
所成角的正弦值.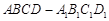 中,
中,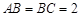 ,过
,过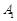 、
、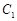 、
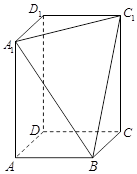
、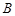 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体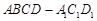 ,且这个几何体的体积为
,且这个几何体的体积为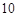 .
.
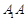 的长;
的长;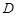 到平面
到平面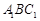 的距离.
的距离.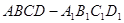 中,面
中,面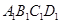 中心为
中心为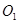 .
.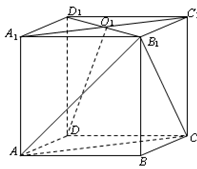
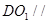 面
面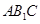 ;
;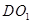 与
与 所成角.
所成角. 的底面是正方形,侧棱与底面边长均为2,则其侧视图的面积为_____.
的底面是正方形,侧棱与底面边长均为2,则其侧视图的面积为_____.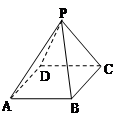
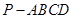 中,
中,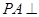 平面
平面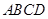 ,四边形
,四边形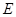 ,
,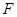 分别是
分别是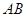 ,
,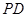 的中点.若
的中点.若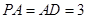 ,
,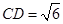 。
。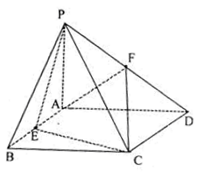
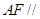 平面
平面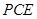 ;
;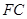 平面
平面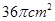 ,则这个球的体积为
,则这个球的体积为 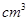 。
。