题目内容
如图所示，点S在平面ABC外，SB⊥AC，SB=AC=2，E、F分别是SC和AB的中点，则EF的长是（ ）
| A．1 | B．
| C．
| D．
|
取BC的中点D，连接ED与FD
∵E、F分别是SC和AB的中点，点D为BC的中点
∴ED∥SB，FD∥AC
而SB⊥AC，SB=AC=2则三角形EDF为等腰直角三角形
则ED=FD=1即EF=
故选：B
∵E、F分别是SC和AB的中点，点D为BC的中点
∴ED∥SB，FD∥AC
而SB⊥AC，SB=AC=2则三角形EDF为等腰直角三角形
则ED=FD=1即EF=
| 2 |
故选：B
练习册系列答案
相关题目
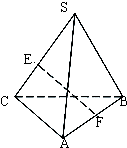如图所示，点S在平面ABC外，SB⊥AC，SB=AC=2，E、F分别是SC和AB的中点，则EF的长是（ ）| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
如图所示，点S在平面ABC外，SB⊥AC，SB=AC=2，E、F分别是SC和AB的中点，则EF=
D．
C．
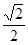D．
