题目内容
若 是函数f(x)=sin 2x+acos2x(a∈R,为常数)的零点,则f(x)的最小正周期是
是函数f(x)=sin 2x+acos2x(a∈R,为常数)的零点,则f(x)的最小正周期是
- A.

- B.π
- C.2π
- D.4π
B
分析:把( ,0)代入函数解析式求出a的值,然后运用三角运算化简整理函数解析式,由三角函数周期公式可求周期.
,0)代入函数解析式求出a的值,然后运用三角运算化简整理函数解析式,由三角函数周期公式可求周期.
解答:因为 是函数f(x)=sin 2x+acos2x(a∈R,为常数)的零点,所以f(
是函数f(x)=sin 2x+acos2x(a∈R,为常数)的零点,所以f( )=sin
)=sin  +acos2
+acos2 =0,
=0,
∴1+ a=0,∴a=-2.
a=0,∴a=-2.
则f(x)=sin 2x+acos2x=sin 2x-2cos2x=sin 2x-cos 2x-1= sin(2x-
sin(2x- )-1.
)-1.
∴f(x)的最小正周期为π.
故选B.
点评:本题考查了函数的周期性和函数的零点概念,考查了三角函数的化简问题,解答此题的关键是三角公式的记忆,是基础题.
分析:把(
 ,0)代入函数解析式求出a的值,然后运用三角运算化简整理函数解析式,由三角函数周期公式可求周期.
,0)代入函数解析式求出a的值,然后运用三角运算化简整理函数解析式,由三角函数周期公式可求周期.解答:因为
 是函数f(x)=sin 2x+acos2x(a∈R,为常数)的零点,所以f(
是函数f(x)=sin 2x+acos2x(a∈R,为常数)的零点,所以f( )=sin
)=sin  +acos2
+acos2 =0,
=0,∴1+
 a=0,∴a=-2.
a=0,∴a=-2.则f(x)=sin 2x+acos2x=sin 2x-2cos2x=sin 2x-cos 2x-1=
 sin(2x-
sin(2x- )-1.
)-1.∴f(x)的最小正周期为π.
故选B.
点评:本题考查了函数的周期性和函数的零点概念,考查了三角函数的化简问题,解答此题的关键是三角公式的记忆,是基础题.

练习册系列答案
相关题目
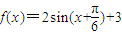 在实数集R上,函数
在实数集R上,函数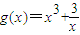 在
在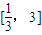 上是不是有界函数?若是,请给出证明;若不是,请说出理由.
上是不是有界函数?若是,请给出证明;若不是,请说出理由.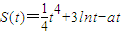 ,要使在
,要使在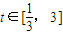 上每一时刻的瞬时速度的绝对值都不大于13,求实数a的取值范围.
上每一时刻的瞬时速度的绝对值都不大于13,求实数a的取值范围.