Question

已知函数f(x)=ax³-x²+1(a为常数).

(1)当a＞0时,求函数f(x)的单调递减区间;

(2)若方程f(x)=0有三个不同的实数解,求实数a的取值范围.

Answer 1

解:(1)f′(x)=3ax²-2x≤0,且a＞0得0≤x≤,

∴f(x)的单调递减区间为［0,］.

(2)显然a≠0,当a＞0时,由(1)知f(x)在(-∞,0］上递增,在［0,］上递减,在［,+∞)上递增,故若f(x)=0有三个实数解,当且仅当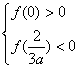0＜a＜.

当a＜0时,同理,可知f(x)在(-∞,］上递减,在［,0］上递增,在［0,+∞)上递减,

故若f(x)=0有三个实数解,当且仅当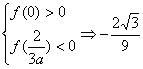＜a＜0.

综上,a∈(,0)∪(0,).