题目内容
(不等式选讲选做题)若ab>0,且A(a,0)、B(0,b)、C(-2,-2)三点共线,则ab的最小值为
16
16
.分析:根据题意,由A、B、C三点共线,可得kAB=kBC,由斜率公式可得2a+2b+ab=0,即ab=-2a-2b,依题意,可得a<0,b<0,则-2a-2b>0,由基本不等式的性质可得-2a-2b≥4
,进而可得,ab≥4
,令t=
>0,可得t2-4t≥0,由一元二次不等式的性质可得t即
的范围,进而易得ab的最小值.
| ab |
| ab |
| ab |
| ab |
解答:解:根据题意,A(a,0)、B(0,b)、C(-2,-2)三点共线,可得kAB=kBC,
即
=
,化简可得2a+2b+ab=0,即ab=-2a-2b,
若ab>0,要么a>0且b>0,要么a<0且b<0
直线经过第三象限的C(-2,-2),由直线的性质可知,a<0,b<0
因为a<0,b<0,所以-2a-2b>0且-2a-2b≥2
=4
,
又因为ab=-2a-2b,所以ab≥4
,
即ab-4
≥0,
令t=
>0,可得t2-4t≥0,
解可得t≥4或t≤0,
又由t>0,则t≥4,
即
≥4,ab≥16;
则ab的最小值为16;
故答案为16.
即
| b-0 |
| 0-a |
| b+2 |
| 0+2 |
若ab>0,要么a>0且b>0,要么a<0且b<0
直线经过第三象限的C(-2,-2),由直线的性质可知,a<0,b<0
因为a<0,b<0,所以-2a-2b>0且-2a-2b≥2
| 4ab |
| ab |
又因为ab=-2a-2b,所以ab≥4
| ab |
即ab-4
| ab |
令t=
| ab |
解可得t≥4或t≤0,
又由t>0,则t≥4,
即
| ab |
则ab的最小值为16;
故答案为16.
点评:本题考查基本不等式的应用,涉及三点共线的问题,有一定的难度;解题的难点在于利用基本不等式对(-2a-2b)变形,可得ab≥4
,进而由一元二次不等式的性质来求解..
| ab |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
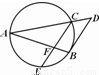
 ,则线段CD的长为 .
,则线段CD的长为 .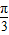 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .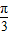 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .