题目内容
当a＞0时，函数f（x）=ax+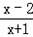
在（﹣1，+∞）是增函数，用反证法证明方程ax+
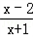=0没有负数根．
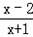在（﹣1，+∞）是增函数，用反证法证明方程ax+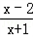=0没有负数根．证明：假设f（x）=0 有负根 x0，且 x0≠-1，即 f（x0）=0．
根据f（0）=1+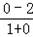
=-1，
可得 f（x0）＞f（0）①．
若-1＜x0＜0，由函数f（x）=ax+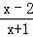
在（-1，+∞）是增函数，
可得f（x0）＜f（0）=-1，这与①矛盾．
若x0＜-1，则
，x0-2＜0，x0+1＜0，
∴f（x0）＞0，这也与①矛盾．
故假设不正确．
∴方程 ax+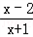
=0 没有负根．
根据f（0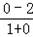）=1+
=-1，可得 f（x0）＞f（0）①．
若-1＜x0＜0，由函数f（x）=ax+
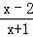在（-1，+∞）是增函数，可得f（x0）＜f（0）=-1，这与①矛盾．
若x0＜-1，则
，x0-2＜0，x0+1＜0，∴f（x0）＞0，这也与①矛盾．
故假设不正确．
∴方程 ax+
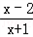=0 没有负根．
练习册系列答案
名校课堂系列答案
相关题目