题目内容
已知f(x)为二次函数,不等式f(x)+2<0的解集为(-1, ),且对任意α,β∈R,恒有f(sinα)≤0,f(2+cosβ)≥0,数列{an}满足a1=1, 3an+1=1-
),且对任意α,β∈R,恒有f(sinα)≤0,f(2+cosβ)≥0,数列{an}满足a1=1, 3an+1=1- (n∈N*)。
(n∈N*)。
(1)求函数f(x)的解析式;
(2)设bn= ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)若(2)中数列{bn}的前n项和为Sn,求数列{Sn·cox(bnπ)}的前n项和Tn。
 ),且对任意α,β∈R,恒有f(sinα)≤0,f(2+cosβ)≥0,数列{an}满足a1=1, 3an+1=1-
),且对任意α,β∈R,恒有f(sinα)≤0,f(2+cosβ)≥0,数列{an}满足a1=1, 3an+1=1- (n∈N*)。
(n∈N*)。(1)求函数f(x)的解析式;
(2)设bn=
 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;(3)若(2)中数列{bn}的前n项和为Sn,求数列{Sn·cox(bnπ)}的前n项和Tn。
解:(1)依题意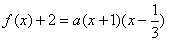
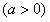
即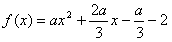
令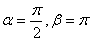
则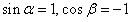
有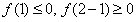
得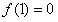
即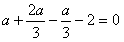
得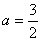
∴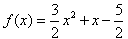 ;
;
(2)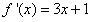
则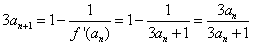
即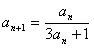
两边取倒数,得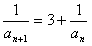
即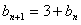
∴数列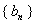 是首项为
是首项为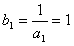 ,公差为的等差数列
,公差为的等差数列
∴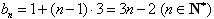 ;
;
(3)∵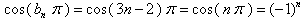
所以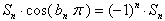
∴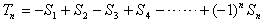
(i)当n为偶数时
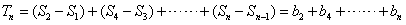
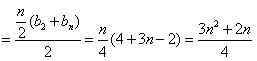
(ii)当n为奇数时
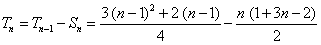
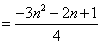
综上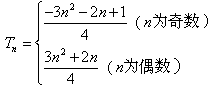 。
。
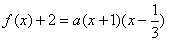
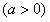
即
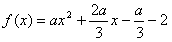
令
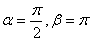
则
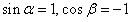
有
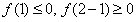
得
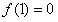
即
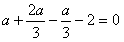
得
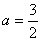
∴
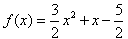 ;
;(2)
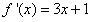
则
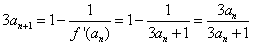
即
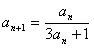
两边取倒数,得
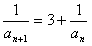
即
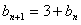
∴数列
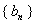 是首项为
是首项为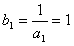 ,公差为的等差数列
,公差为的等差数列∴
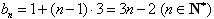 ;
;(3)∵
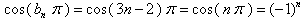
所以
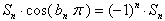
∴
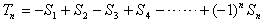
(i)当n为偶数时
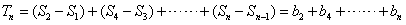
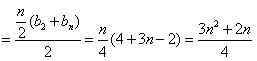
(ii)当n为奇数时
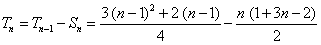
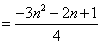
综上
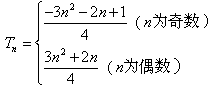 。
。
练习册系列答案
相关题目