题目内容
若 ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
B
解析试题分析:因为 ……①,所以两边平方,得:
……①,所以两边平方,得:
 ……②
……②
①②联立,得: ,所以
,所以 ,所以
,所以
 。
。
考点:同角三角函数关系式;和差公式。
点评:此题也可以这样做:因为 ,所以与
,所以与 联立:
联立: ,由此可以解得
,由此可以解得 的值,从而就可以解得
的值,从而就可以解得 的值。联立组成方程组,这是最基本的方法,其优点是思维含量较少,缺点是计算量大。平方后联立方程组的优点是计算量小,缺点是思维含量大。
的值。联立组成方程组,这是最基本的方法,其优点是思维含量较少,缺点是计算量大。平方后联立方程组的优点是计算量小,缺点是思维含量大。

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
若 ,则
,则 = ( )
= ( )
A. | B. | C.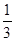 | D. |
若函数 的图象(部分)如图所示,则
的图象(部分)如图所示,则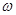 和
和 的取值是
的取值是 
A. | B. |
C.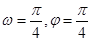 | D. |
设α是第二象限角,P(x,4)为其终边上的一点,且 ,则
,则 =( )
=( )
A. | B. | C. | D. |
将函数 的图像沿
的图像沿 轴向右平移
轴向右平移 个单位
个单位 ,所得图像关于
,所得图像关于 轴对称,则
轴对称,则 的最小值为
的最小值为
A. | B. | C. | D. |
要得到函数 的图像, 需要将函数
的图像, 需要将函数 的图像( )
的图像( )
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
当 时,函数
时,函数 取得最小值,则函数
取得最小值,则函数 是( )
是( )
A.奇函数且图像关于点 对称 对称 | B.偶函数且图像关于点 对称 对称 |
C.奇函数且图像关于直线 对称 对称 | D.偶函数且图像关于点 对称 对称 |
若角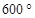 的终边上有一点
的终边上有一点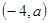 ,则
,则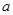 的值是.
的值是.
A. | B. | C. | D. |
 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是