Question

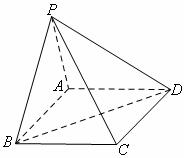
（08年天津卷）（本小题满分12分）如图，在四棱锥中，底面是矩形．已知．

（Ⅰ）证明平面；

（Ⅱ）求异面直线与所成的角的大小；

（Ⅲ）求二面角的大小．

Answer 1

本小题主要考查直线和平面垂直，异面直线所成的角、二面角等基础知识，考查空间想象能力，运算能力和推理论证能力．满分12分．

（Ⅰ）证明：在中，由题设可得

于是.在矩形中，.又，

所以平面．

（Ⅱ）解：由题设，，所以（或其补角）是异面直线与所成的角.

在中，由余弦定理得

 

 

由（Ⅰ）知平面，平面，

所以，因而，于是是直角三角形，故．

所以异面直线与所成的角的大小为．

（Ⅲ）解：过点P做于H，过点H做于E，连结PE

因为平面，平面，所以.又，

因而平面，故HE为PE再平面ABCD内的射影.由三垂线定理可知，

，从而是二面角的平面角。

由题设可得，

于是再中，

所以二面角的大小为．