题目内容
已知四个首尾相接的向量,若第一个向量的起点为平面凸四边形ABCD的顶点A,每个向量的终点都是随机选取与该向量起点相邻的顶点.(I)列举这四个向量终点的排列方式;
(II)求这四个向量之和为
| 0 |
分析:(I)首先用列举法列举所有满足条件的向量,
(II)再分析这些向量中这四个向量之和为
的排列方式的情况与数目,最后得到满足条件的数目,利用古典概型概率计算公式计算即可
(II)再分析这些向量中这四个向量之和为
| 0 |
解答:解:根据题意,
(I)可能的情况有BABC,BABA,BADA,BADC,BCDA,BCDC,BCBA,BCBC,DABA,DABC,DADA,DADC,DCBA,DCBC,DCDA,DCDC共有16种
(II)四个向量之和为
,则第四个向量的终点必为点A,由(I)知共8种,且每种等可能
∴这四个向量之和为
的概率为:
=
(I)可能的情况有BABC,BABA,BADA,BADC,BCDA,BCDC,BCBA,BCBC,DABA,DABC,DADA,DADC,DCBA,DCBC,DCDA,DCDC共有16种
(II)四个向量之和为
| 0 |
∴这四个向量之和为
| 0 |
| 8 |
| 16 |
| 1 |
| 2 |
点评:本题考查古典概型及其概率计算公式,计数原理的应用,注意按一定的规律顺序,作到不重不漏,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
选择题:
(1)
在四边形ABCD中,若 ,则四边形ABCD是
,则四边形ABCD是
[
]|
A .矩形 |
B .菱形 |
|
C .正方形 |
D .平行四边形 |
(2)
已知向量 ,
,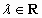 ,
,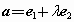 ,
,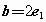 ,若向量a与b共线,则
,若向量a与b共线,则
[
]|
A . |
B . |
|
C . |
D . 或 或 |
(3)
已知a,b为两个单位向量,下列四个命题中正确的是[
]A
.a与b相等B
.如果a与b平行,那么a与b相等C
.a与b共线D
.如果a与b平行,那么a=b或a=-b(4)已知两个力 ,
, 的夹角为
的夹角为 ,它们的合力大小为10N,合力与
,它们的合力大小为10N,合力与 的夹角为
的夹角为 ,那么
,那么 的大小为
的大小为
[
]|
A . N N |
B .5N |
|
C .10N |
D . N N |
(5)
已知向量a表示“向东航行3km”,b表示“向南航行3km”,则a+b表示[
]|
A .向东南航行6km |
B .向东南航行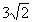 km km |
|
C .向东北航行 km km |
D .向东北航行6km |
(6)
河水的流速为2m/s,一艘小船想沿垂直于河岸方向以10m/s的速度驶向对岸,则小船的静水速度大小为[
]|
A .10m/s |
B . m/s m/s |
|
C . m/s m/s |
D .12m/s |
 的概率.
的概率. 的概率.
的概率.