题目内容
已知定义在R上的奇函数f(x)在(0,+∞)上是增函数,且f(ax+1)≤f(x-2)对任意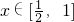 都成立,则实数a的取值范围是________.
都成立,则实数a的取值范围是________.
(-∞,-5]
分析:根据奇函数在对称区间上单调性相同结合已知可得f(x)在(-∞,+∞)上是增函数,进而可将f(ax+1)≤f(x-2)对任意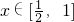 都成立,转化为ax+1≤x-2对任意
都成立,转化为ax+1≤x-2对任意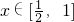 都成立,即a≤
都成立,即a≤ =1-
=1- 对任意
对任意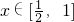 都成立,即a小于等于函数y=1-
都成立,即a小于等于函数y=1- 在
在 的最小值,利用单调性法求出函数y=1-
的最小值,利用单调性法求出函数y=1- 在
在 的最小值,可得实数a的取值范围
的最小值,可得实数a的取值范围
解答:根据奇函数在对称区间上单调性相同且f(x)在(0,+∞)上是增函数,
故f(x)在(-∞,+∞)上是增函数,
若f(ax+1)≤f(x-2)对任意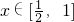 都成立,
都成立,
则ax+1≤x-2对任意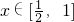 都成立,
都成立,
即a≤ =1-
=1- 对任意
对任意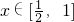 都成立,
都成立,
由函数y=1- 在
在 为增函数,
为增函数,
故x= 时,最最小值-5
时,最最小值-5
即a≤-5
故实数a的取值范围是(-∞,-5]
故答案为:(-∞,-5]
点评:本题考查的知识点是函数的单调性,函数的奇偶性,函数恒成立问题,是函数图象和性质的综合应用,难度中档.
分析:根据奇函数在对称区间上单调性相同结合已知可得f(x)在(-∞,+∞)上是增函数,进而可将f(ax+1)≤f(x-2)对任意
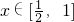 都成立,转化为ax+1≤x-2对任意
都成立,转化为ax+1≤x-2对任意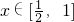 都成立,即a≤
都成立,即a≤ =1-
=1- 对任意
对任意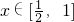 都成立,即a小于等于函数y=1-
都成立,即a小于等于函数y=1- 在
在 的最小值,利用单调性法求出函数y=1-
的最小值,利用单调性法求出函数y=1- 在
在 的最小值,可得实数a的取值范围
的最小值,可得实数a的取值范围解答:根据奇函数在对称区间上单调性相同且f(x)在(0,+∞)上是增函数,
故f(x)在(-∞,+∞)上是增函数,
若f(ax+1)≤f(x-2)对任意
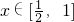 都成立,
都成立,则ax+1≤x-2对任意
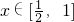 都成立,
都成立,即a≤
 =1-
=1- 对任意
对任意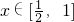 都成立,
都成立,由函数y=1-
 在
在 为增函数,
为增函数,故x=
 时,最最小值-5
时,最最小值-5即a≤-5
故实数a的取值范围是(-∞,-5]
故答案为:(-∞,-5]
点评:本题考查的知识点是函数的单调性,函数的奇偶性,函数恒成立问题,是函数图象和性质的综合应用,难度中档.

练习册系列答案
相关题目
 ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函 B.
B.

 D.
D.

 ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)
 时,f(cosθ+msinθ)+f(-2m-2)<0恒成立,求实数m的取值范围.
时,f(cosθ+msinθ)+f(-2m-2)<0恒成立,求实数m的取值范围.