题目内容
设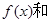
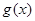 是定义在R上的两个函数,
是定义在R上的两个函数,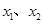 是R上任意两个不等的实根,设
是R上任意两个不等的实根,设
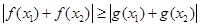 恒成立,且
恒成立,且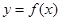 为奇函数,判断函数
为奇函数,判断函数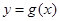 的奇偶性并说明理由。
的奇偶性并说明理由。
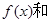
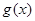 是定义在R上的两个函数,
是定义在R上的两个函数,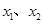 是R上任意两个不等的实根,设
是R上任意两个不等的实根,设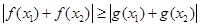 恒成立,且
恒成立,且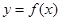 为奇函数,判断函数
为奇函数,判断函数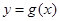 的奇偶性并说明理由。
的奇偶性并说明理由。函数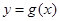 为奇函数,见解析。
为奇函数,见解析。
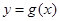 为奇函数,见解析。
为奇函数,见解析。本试题主要是考查了函数的奇偶性的证明。
先分析令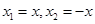 ,所以
,所以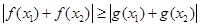 即为
即为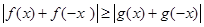
又由已知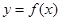 为奇函数,故
为奇函数,故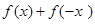 =0
=0
所以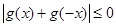 ,可知
,可知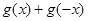 =0对任意的
=0对任意的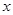 都成立得到结论。
都成立得到结论。
证明:函数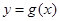 为奇函数
为奇函数
以下证明:令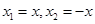 ,………………………………….1分
,………………………………….1分
所以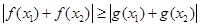 即为
即为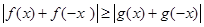 。。。。。。。2分
。。。。。。。2分
又由已知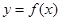 为奇函数,故
为奇函数,故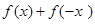 =0
=0
所以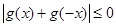 ,可知
,可知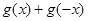 =0对任意的
=0对任意的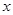 都成立,。。。。。。。。。。。4分
都成立,。。。。。。。。。。。4分
又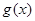 是定义在R上的函数,定义域关于原点对称 ∴函数
是定义在R上的函数,定义域关于原点对称 ∴函数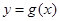 为奇函数。。。。6分
为奇函数。。。。6分
先分析令
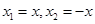 ,所以
,所以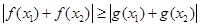 即为
即为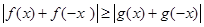
又由已知
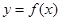 为奇函数,故
为奇函数,故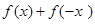 =0
=0所以
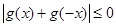 ,可知
,可知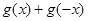 =0对任意的
=0对任意的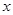 都成立得到结论。
都成立得到结论。证明:函数
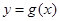 为奇函数
为奇函数以下证明:令
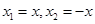 ,………………………………….1分
,………………………………….1分所以
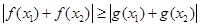 即为
即为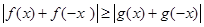 。。。。。。。2分
。。。。。。。2分又由已知
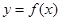 为奇函数,故
为奇函数,故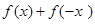 =0
=0所以
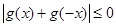 ,可知
,可知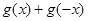 =0对任意的
=0对任意的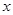 都成立,。。。。。。。。。。。4分
都成立,。。。。。。。。。。。4分又
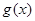 是定义在R上的函数,定义域关于原点对称 ∴函数
是定义在R上的函数,定义域关于原点对称 ∴函数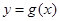 为奇函数。。。。6分
为奇函数。。。。6分
练习册系列答案
相关题目
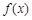 是定义在R上的奇函数,当
是定义在R上的奇函数,当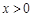 时,
时,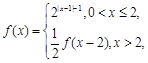 则函数
则函数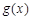 =
=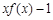 在
在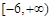 上的所有零点之和为
上的所有零点之和为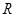 上的偶函数
上的偶函数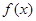 在区间
在区间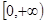 上是单调递增,若
上是单调递增,若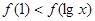 ,则
,则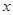 的取值范围是
的取值范围是 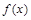 是定义在R上的奇函数,满足
是定义在R上的奇函数,满足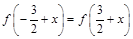 .当
.当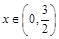 时,
时,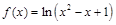 ,则函数
,则函数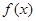 为定义域在
为定义域在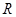 上的奇函数,当
上的奇函数,当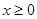 时,
时,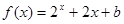 (
(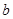 为常数),则
为常数),则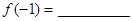
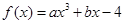 其中
其中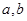 为常数,若
为常数,若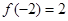 ,则
,则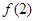 =
= 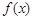 是定义在
是定义在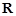 上且周期为2的函数,在区间
上且周期为2的函数,在区间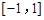 上,
上,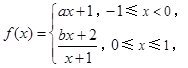 其中
其中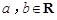 .若
.若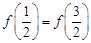 ,则
,则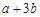 的值为 .
的值为 .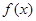 满足
满足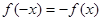 ,并且当
,并且当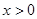 时,
时,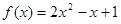 ,则当
,则当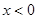 时,
时,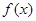 是定义在
是定义在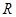 上且以3为周期的奇函数,当
上且以3为周期的奇函数,当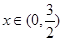 时,
时,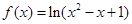 ,则函数
,则函数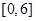 上的零点个数是( )
上的零点个数是( )