题目内容
(3分)(2011•重庆)设m,k为整数,方程mx2﹣kx+2=0在区间(0,1)内有两个不同的根,则m+k的最小值为( )
| A.﹣8 | B.8 | C.12 | D.13 |
D
解析试题分析:将一元二次方程的根的分布转化为确定相应的二次函数的图象来处理,根据图象可得到关于m和k的不等式组,此时不妨考虑利用不等式所表示的平面区域来解决,但须注意这不是线性规划问题,同时注意取整点.
解:设f(x)=mx2﹣kx+2,由f(0)=2,易知f(x)的图象恒过定点(0,2),
因此要使已知方程在区间(0,1)内两个不同的根,即f(x)的图象在区间(0,1)内与x轴有两个不同的交点
即由题意可以得到:必有 ,即
,即 ,
,
在直角坐标系mok中作出满足不等式平面区域,
如图所示,设z=m+k,则直线m+k﹣z=0经过图中的阴影中的整点(6,7)时,
z=m+k取得最小值,即zmin=13.
故选D.
点评:此题考查了二次函数与二次方程之间的联系,解答要注意几个关键点:(1)将一元二次方程根的分布转化一元二次函数的图象与x轴的交点来处理;(2)将根据不等式组求两个变量的最值问题处理为规划问题;(3)作出不等式表示的平面区域时注意各个不等式表示的公共区域;(4)不可忽视求得最优解是整点.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案直线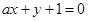 与连接
与连接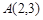 ,
,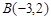 的线段相交,则
的线段相交,则 的取值范围是( )
的取值范围是( )
A.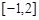 | B.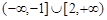 |
C.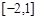 | D.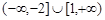 |
若实数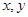 满足条件
满足条件 ,则
,则 的最大值为( )
的最大值为( )
| A.9 | B.11 | C.12 | D.16 |
若不等式组 表示的平面区域是一个钝角三角形,则实数
表示的平面区域是一个钝角三角形,则实数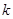 的取值范围( )
的取值范围( )
A.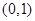 | B.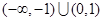 | C.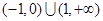 | D. |
[2013·福建高考]若变量x,y满足约束条件 则z=2x+y的最大值和最小值分别为( )
则z=2x+y的最大值和最小值分别为( )
| A.4和3 | B.4和2 | C.3和2 | D.2和0 |
(2011•浙江)设实数x、y满足不等式组 ,若x、y为整数,则3x+4y的最小值是( )
,若x、y为整数,则3x+4y的最小值是( )
| A.14 | B.16 | C.17 | D.19 |
若点(x,y)位于曲线y = |x|与y = 2所围成的封闭区域, 则2x-y的最小值为
| A.-6 | B.-2 | C.0 | D.2 |
设 ,在约束条件
,在约束条件 下,目标函数
下,目标函数 的最大值小于2,则
的最大值小于2,则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
设x、y满足 则
则 ( )
( )
| A.有最小值2,最大值3 |
| B.有最小值2,无最大值 |
| C.有最小值3,无最大值 |
| D.既无最小值,也无最大值 |