题目内容
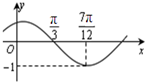已知函数f（x）=Asin（ωx+Φ）（其中A＞0，|Φ|＜| π | 2 |
（1）求函数f（x）的解析式；
（2）求f（x）的单调区间．
分析：（1）由图象的顶点坐标求出A，由周期求出ω，通过图象经过（
，0），求出φ，从而得到f（x）的解析式．
（2）通过（1）函数的解析式直接利用正弦函数的单调增区间与单调减区间求出函数的单调区间即可．
| π |
| 3 |
（2）通过（1）函数的解析式直接利用正弦函数的单调增区间与单调减区间求出函数的单调区间即可．
解答：解：（1）由函数的图象可得A=1，T=4×（
-
）=π，
T=
，
解得ω=2．
图象经过（
，0），0=sin（2×
+φ），|φ|＜
，φ=
，
故f（x）的解析式为 f（x）=sin（2x+
）．
（2）由2kπ+
≤2x+
≤2kπ+
，k∈z，
可得 kπ+
≤x≤kπ+
π，k∈Z，
故函数y=sin（2x+
）的单调递减区间是[kπ+
π，kπ+
π]，k∈Z，
同理可得函数的单调增区间[kπ-
π，kπ+
π]，k∈Z．
| 7π |
| 12 |
| π |
| 3 |
T=
| 2π |
| ω |
解得ω=2．
图象经过（
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
故f（x）的解析式为 f（x）=sin（2x+
| π |
| 3 |
（2）由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
可得 kπ+
| π |
| 12 |
| 7 |
| 12 |
故函数y=sin（2x+
| π |
| 3 |
| π |
| 12 |
| 7 |
| 12 |
同理可得函数的单调增区间[kπ-
| 5π |
| 12 |
| π |
| 12 |
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求函数的解析式，注意函数的周期的求法，考查函数的单调区间的求法，考查计算能力．
练习册系列答案
计算高手系列答案
相关题目