题目内容
任意a、b∈R,定义运算a*b=
,则f(x)=x*ex的( )
|
| A、最小值为-e | ||
B、最小值为-
| ||
C、最大值为-
| ||
| D、最大值为e |
分析:先由定义求出f(x)的表达式,在利用分段函数求值域分段找的方法求出函数的最值.
解答:解:由题中定义可得f(x)=
,
∴f′(x)=
,
当x≤0时,f(x)在(-∞,-1)上为增函数,在(-1,0)上为减函数,
所以f(x)在x=-1时取极小值f(-1)=-
,
当x>0时,f(x)在(1,+∞)上为增函数,在(0,1)上为减函数,
所以f(x)在x=1时取极小值f(1)=-
,
又因为f(-1)=f(1)=-
,
所以f(x)=x*ex的最小值为-
,
故选 B.
|
∴f′(x)=
|
当x≤0时,f(x)在(-∞,-1)上为增函数,在(-1,0)上为减函数,
所以f(x)在x=-1时取极小值f(-1)=-
| 1 |
| e |
当x>0时,f(x)在(1,+∞)上为增函数,在(0,1)上为减函数,
所以f(x)在x=1时取极小值f(1)=-
| 1 |
| e |
又因为f(-1)=f(1)=-
| 1 |
| e |
所以f(x)=x*ex的最小值为-
| 1 |
| e |
故选 B.
点评:本题在考查新定义的基础上,又考查了分段函数求值域的方法,关于新定义的题,关键在于理解新定义,并会用新定义解题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
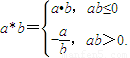 ,则f(x)=x*ex的( )
,则f(x)=x*ex的( )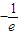
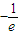
 ,则f(x)=x*ex的( )
,则f(x)=x*ex的( )
