题目内容
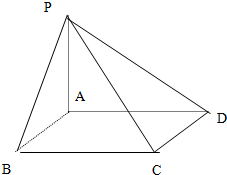如图，四边形ABCD是矩形，PA⊥平面ABCD，其中AB=3，PA=4，若在线段PD上存在点E使得BE⊥CE，求线段AD的取值范围，并求当线段PD上有且只有一个点E使得BE⊥CE时，二面角E-BC-A正切值的大小．分析：根据题意，以BC为直径的球与线段PD有交点，因此设BC的中点为O（即球心），取AD的中点M，连接OM，作ME⊥PD于点E，连接OE．要使以BC为直径的球与PD有交点，只要OE≤OC即可，设OC=OB=R，算出ME=
，从而得到OE2=9+
≤R2，解此不等式得R≥2
，所以AD的取值范围[4
，+∞）．最后根据AD=4
时，点E在线段PD上惟一存在，结合二面角平面角的定义和题中数据，易得此时二面角E-BC-A正切值．
| 4R | ||
|
| 4R2 |
| 4+R2 |
| 3 |
| 3 |
| 3 |
解答：解：若以BC为直径的球面与线段PD有交点E，由于点E与BC确定的平面与球的截面是一个大圆，则必有BE⊥CE，因此问题
转化为以BC为直径的球与线段PD有交点．
设BC的中点为O（即球心），再取AD的中点M，
∵AB⊥AD，AB⊥AP，AP∩AD=A，∴AB⊥平面PAD，
∵矩形ABCD中，O、M是对边中点的连线
∴OM∥AB，可得OM⊥平面PAD，
作ME⊥PD交PD于点E，连接OE，
则OE⊥PD，所以OE即为点O到直线PD的距离，
又∵OD＞OC，OP＞OA＞OB，点P，D在球O外，
∴要使以BC为直径的球与线段PD有交点，只要使OE≤OC（设OC=OB=R）即可．
由于△DEM∽△DAP，可求得ME=
，
∴OE2=9+ME2=9+
令OE2≤R2，即9+
≤R2，解之得R≥2
；
∴AD=2R≥4
，得AD的取值范围[4
，+∞），
当且仅当AD=4
时，点E在线段PD上惟一存在，
此时作EH∥PA交AD于H，再作HK⊥BC于K，连接EK，
可得BC⊥平面EHK，∠EKH即为二面角E-BC-A的平面角
∵以BC为直径的球半径R=2
=OE，∴ME=
=
，
由此可得ED=
=3，所以EH=
=
=
∵PA⊥平面ABCD，EH∥PA，∴EH⊥平面ABCD，得EH⊥HK
∵Rt△EHK中，HK=AB=3，∴tan∠EKH=
=
即二面角E-BC-A的平面角正切值为
．
转化为以BC为直径的球与线段PD有交点．设BC的中点为O（即球心），再取AD的中点M，
∵AB⊥AD，AB⊥AP，AP∩AD=A，∴AB⊥平面PAD，
∵矩形ABCD中，O、M是对边中点的连线
∴OM∥AB，可得OM⊥平面PAD，
作ME⊥PD交PD于点E，连接OE，
则OE⊥PD，所以OE即为点O到直线PD的距离，
又∵OD＞OC，OP＞OA＞OB，点P，D在球O外，
∴要使以BC为直径的球与线段PD有交点，只要使OE≤OC（设OC=OB=R）即可．
由于△DEM∽△DAP，可求得ME=
| 4R | ||
|
∴OE2=9+ME2=9+
| 4R2 |
| 4+R2 |
令OE2≤R2，即9+
| 4R2 |
| 4+R2 |
| 3 |
∴AD=2R≥4
| 3 |
| 3 |
当且仅当AD=4
| 3 |
此时作EH∥PA交AD于H，再作HK⊥BC于K，连接EK，
可得BC⊥平面EHK，∠EKH即为二面角E-BC-A的平面角
∵以BC为直径的球半径R=2
| 3 |
| 4R | ||
|
| 3 |
由此可得ED=
| EM×AD |
| PA |
| PA×DE |
| PD |
| 4×3 | ||||
|
| 3 |
| 2 |
∵PA⊥平面ABCD，EH∥PA，∴EH⊥平面ABCD，得EH⊥HK
∵Rt△EHK中，HK=AB=3，∴tan∠EKH=
| EH |
| HK |
| 1 |
| 2 |
即二面角E-BC-A的平面角正切值为
| 1 |
| 2 |
点评：本题给出特殊四棱锥，探索空间两条直线相互垂直的问题，并求二面角的正切值，着重考查了空间垂直位置关系的证明和二面角平面角的作法，以及求二面角大小等知识点，属于中档题．
练习册系列答案
相关题目
如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，A′A⊥平面ABCD．
如图，四边形ABCD为正方形，QA⊥平面ABCD，PD∥QA，QA=AB=
如图，四边形ABCD为矩形，且AD=2，AB=1，PA⊥平面ABCD，PA=1，E为BC的中点．
如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=