题目内容
已知函数 ,
, ,给出下列命题:
,给出下列命题:
①函数y=f(x)g(x)的最小正周期为2π;
②函数y=f(x)-g(x)的最大值是 ;
;
③函数y=f(2x)的图象可由y=g(2x)的图象向左平移 个单位得到;
个单位得到;
④函数y=f(2x)的图象可由y=g(2x)的图象向右平移 个单位得到.
个单位得到.
其中正确命题的序号是 ________.(写出所有正确命题的序号)
②④
分析:对f(x)g(x)根据诱导公式和二倍角公式进行化简,进而可求出其最小正周期可判断①;根据诱导公式和两角和与差的公式进行化简,进而可求得最大值,可判断②;根据三角函数平移的左加右减原则进行平移可判断③和④.
解答:∵f(x)g(x)=cos(x+ )sin(x-
)sin(x- )=sinxcosx=
)=sinxcosx= sin2x
sin2x
∴T= ,故①不对;
,故①不对;
∵y=f(x)-g(x)=cos(x+ )-sin(x-
)-sin(x- )=cosx-sinx=
)=cosx-sinx= cos(x+
cos(x+ )
)
∴y=f(x)-g(x)的最大值为 ,故②正确;
,故②正确;
将y=g(2x)=sin(2x- )向左平移
)向左平移 得到y=sin[2(x+
得到y=sin[2(x+ )-
)- ]=sin2x
]=sin2x
又∵y=f(2x)=cos(2x+ )=-sin2x
)=-sin2x
故③不对;
将y=g(2x)=sin(2x- )向右平移
)向右平移 得到y=sin[2(x-
得到y=sin[2(x- )-
)- ]=-sin2x
]=-sin2x
又∵y=f(2x)=cos(2x+ )=-sin2x
)=-sin2x
故④正确
故答案为:②④.
点评:本题主要考查三角函数的最小正周期、最值和三角函数的平移问题.考查基础知识的综合应用和灵活应用能力.对三角函数的考查以基础题为主,平时要注意基础知识的积累和练习.
分析:对f(x)g(x)根据诱导公式和二倍角公式进行化简,进而可求出其最小正周期可判断①;根据诱导公式和两角和与差的公式进行化简,进而可求得最大值,可判断②;根据三角函数平移的左加右减原则进行平移可判断③和④.
解答:∵f(x)g(x)=cos(x+
 )sin(x-
)sin(x- )=sinxcosx=
)=sinxcosx= sin2x
sin2x∴T=
 ,故①不对;
,故①不对;∵y=f(x)-g(x)=cos(x+
 )-sin(x-
)-sin(x- )=cosx-sinx=
)=cosx-sinx= cos(x+
cos(x+ )
)∴y=f(x)-g(x)的最大值为
 ,故②正确;
,故②正确;将y=g(2x)=sin(2x-
 )向左平移
)向左平移 得到y=sin[2(x+
得到y=sin[2(x+ )-
)- ]=sin2x
]=sin2x又∵y=f(2x)=cos(2x+
 )=-sin2x
)=-sin2x故③不对;
将y=g(2x)=sin(2x-
 )向右平移
)向右平移 得到y=sin[2(x-
得到y=sin[2(x- )-
)- ]=-sin2x
]=-sin2x又∵y=f(2x)=cos(2x+
 )=-sin2x
)=-sin2x故④正确
故答案为:②④.
点评:本题主要考查三角函数的最小正周期、最值和三角函数的平移问题.考查基础知识的综合应用和灵活应用能力.对三角函数的考查以基础题为主,平时要注意基础知识的积累和练习.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 ,现给出下列命题:
,现给出下列命题: =
= ;
; 在
在 上是增函数;
上是增函数;  时,不等式
时,不等式 恒成立;
恒成立; 是偶函数.
是偶函数. ,现给出下列命题:
,现给出下列命题: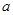 =
= ;
;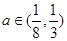 时,不等式
时,不等式 恒成立
恒成立 是偶函数
是偶函数 ,现给出下列命题:
,现给出下列命题: =
=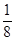 ;
; 时,不等式
时,不等式 恒成立;
恒成立;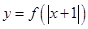 是偶函数 . 其中正确的命题是 ( )
是偶函数 . 其中正确的命题是 ( ) ,现给出下列命题:
,现给出下列命题: ;
; 时,不等式f(1+a)•f(1-a)<0恒成立;
时,不等式f(1+a)•f(1-a)<0恒成立; ,现给出下列命题:
,现给出下列命题: ;
; 时,不等式f(1+a)•f(1-a)<0恒成立;
时,不等式f(1+a)•f(1-a)<0恒成立;