题目内容
已知
是定义在
上的不恒为零的函数，且对任意的
都满足：
，若
，
（
），求证：
．
证明见解析
解析:
证明：令
，
当
时，；当
时，
；
当
时，
；
猜想
， 
用数学归纳法证明如下：
当时，
，式成立，
假设
时，式成立，即
，当
时，
，
时，式成立．
由（1）（2）知，对，
成立，
所以
．
要证明结论成立，只需证明
，
，
．
练习册系列答案
相关题目
解析:
题目内容
已知是定义在上的不恒为零的函数，且对任意的都满足：，若，（），求证：．
证明见解析
证明：令，
当时，；当时，；
当时，；
猜想，
用数学归纳法证明如下：
当时，，式成立，
假设时，式成立，即，当时，
，
时，式成立．
由（1）（2）知，对，成立，
所以．
要证明结论成立，只需证明，
，
．
（其中
）是偶函数，则实数
；
既是奇函数又是偶函数；
的减区间是
；
是定义在
上的不恒为零的函数，且对任意的
都满足
，则
是定义在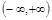
上的不恒为零的函数，且对定义域内的任意x, y, f (x)都满足
．
（
为不为零的常数）
是定义在
上的不恒为零的函数，且对任意
满足下列关系式：
，
，
，
；
②
为等比数列； 
为等差数列。其中正确的结论是：_____ __。（将所有正确命题的序号都填上）
是定义在
上的不恒为零的函数，且对任意
满足下列关系式：
，
，
，
，考察下列结论：①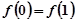
，②
为等比数列 ，④数列
为等差数列，其中正确的结论有_