题目内容
函数
是偶函数，则a=________．
-1
分析：将f（x）=asin（x+
）+
sin（x-
）转化为f（x）=
（a+1）sinx+（
-
）cosx，利用偶函数的概念可求得a的值．
解答：∵f（x）=asin（x+）+sin（x-）
=a（sinx+
cosx）+（sinx-cosx）
=（a+1）sinx+（-）cosx为偶函数，
∴f（-x）=f（x），
∴a+1=0，
∴a=-1．
故答案为：-1．
点评：本题考查三角函数的化简，考查函数的奇偶性，求得f（x）=（a+1）sinx+（-）cosx是关键，属于中档题．
分析：将f（x）=asin（x+
）+sin（x-）转化为f（x）=（a+1）sinx+（-）cosx，利用偶函数的概念可求得a的值．解答：∵f（x）=asin（x+
）+sin（x-）=a（
sinx+cosx）+（sinx-cosx）=
（a+1）sinx+（-）cosx为偶函数，∴f（-x）=f（x），
∴a+1=0，
∴a=-1．
故答案为：-1．
点评：本题考查三角函数的化简，考查函数的奇偶性，求得f（x）=
（a+1）sinx+（-）cosx是关键，属于中档题． 
练习册系列答案
相关题目
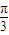个单位长度后得到的图象对应的函数是偶函数，则a的值为 ．
是偶函数，则a=_______________。
是偶函数，则a可取值的集合是 （
）