题目内容
16.（本小题满分8分）直线l过直线x + y－2 = 0和直线x－y + 4 = 0的交点，且与直线3x－2y + 4 = 0平行，求直线l的方程.
【答案】
解法一：联立方程：
解得 
，即直线l过点(－1,3)，
由直线l与直线3x－2y + 4 = 0平行得：直线l的斜率为，
所以直线l的方程为：y－3 = (x + 1) 即3x－2y + 9 = 0.
解法二：∵直线x + y－2 = 0不与3x－2y + 4 = 0平行
∴可设符合条件的直线l的方程为：x－y + 4 + λ(x + y－2)= 0
整理得：(1 + λ)x + (λ－1)y + 4－2λ = 0
∵直线l与直线3x－2y + 4 = 0平行
∴ 解得λ =
∴直线l的方程为：x－ y + = 0 即3x－2y + 9 = 0
【解析】略
练习册系列答案
相关题目
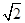＝1．414，
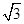＝1．732，
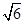＝2．449）．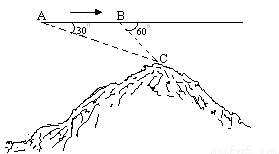
中，
，
，
分别为棱
、
的中点，
为棱
上的点。
；
时，求二面角
的大小。
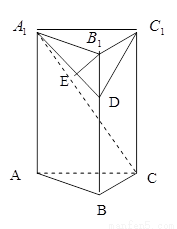
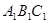中，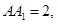
AB = 1,
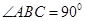；点D、E分别在
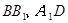上，且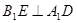
，
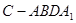与直三棱柱的体积之比为3：5。
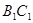的距离；(8分)
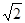，求二面角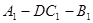
的平面角的正切值。(5分)
