题目内容
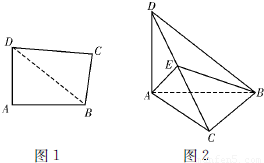 如图l,四边形ABCD中,AB=AD,AB⊥AD,DC⊥BC,将△DCB沿BD折起,使AC⊥BC,如图2.点E在DC上,AE=
如图l,四边形ABCD中,AB=AD,AB⊥AD,DC⊥BC,将△DCB沿BD折起,使AC⊥BC,如图2.点E在DC上,AE=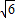 且AE⊥DC,若二面角A-BD-C的正弦值为
且AE⊥DC,若二面角A-BD-C的正弦值为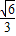 .
.(1)求证:AE⊥BD;
(2)求三棱锥D-ABE的体积.
【答案】分析:(1)由已知先证BC⊥平面ACD,则BC⊥AE,结合AE⊥DC,可证得AE⊥平面BCD,再由线面垂直的定义证得AE⊥BD;
(2)三棱锥D-ABE的体积,即三棱锥A-BDE的体积,求出三角形BDE的面积,代入棱锥体积公式,可得答案.
解答: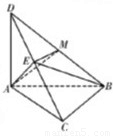 证明:(1)∵AC⊥BC,DC⊥BC,AC∩DC=C
证明:(1)∵AC⊥BC,DC⊥BC,AC∩DC=C
∴BC⊥平面ACD
又∵AE?平面ACD
∴BC⊥AE
又∵AE⊥DC,DC∩BC=C
故AE⊥平面BCD
又∵BD?平面BCD
∴AE⊥BD;
(2)取BD的中点M,连接AM,EM,
∵AB=AD,则AM⊥BD
又∵AE⊥BD,AM∩AE=A
∴BD⊥平面AEM∴EM⊥BD
∴∠AME即为二面角A-BD-C的平面角
在Rt△AEM中,AE=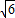 ,AM=
,AM=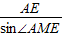 =
=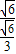 =3,EM=
=3,EM=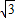
又∵AB=AD,AB⊥AD,故△ABD为等腰直角三角形,故DB=6
∴三棱锥D-ABE的体积VD-ABE=VA-DBE= •
• •EM•DB•AE=3
•EM•DB•AE=3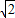
点评:本题考查的知识点是二面角的平面角求求法,棱锥的体积,空间中直线与直线的位置关系,(1)要熟练掌握空间线线垂直与线面垂直之间的相互转化,(2)的关键是构造出二面角的平面角,然后解三角形求出棱锥的棱长.
(2)三棱锥D-ABE的体积,即三棱锥A-BDE的体积,求出三角形BDE的面积,代入棱锥体积公式,可得答案.
解答:
 证明:(1)∵AC⊥BC,DC⊥BC,AC∩DC=C
证明:(1)∵AC⊥BC,DC⊥BC,AC∩DC=C∴BC⊥平面ACD
又∵AE?平面ACD
∴BC⊥AE
又∵AE⊥DC,DC∩BC=C
故AE⊥平面BCD
又∵BD?平面BCD
∴AE⊥BD;
(2)取BD的中点M,连接AM,EM,
∵AB=AD,则AM⊥BD
又∵AE⊥BD,AM∩AE=A
∴BD⊥平面AEM∴EM⊥BD
∴∠AME即为二面角A-BD-C的平面角
在Rt△AEM中,AE=
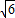 ,AM=
,AM=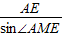 =
=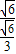 =3,EM=
=3,EM=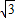
又∵AB=AD,AB⊥AD,故△ABD为等腰直角三角形,故DB=6
∴三棱锥D-ABE的体积VD-ABE=VA-DBE=
 •
• •EM•DB•AE=3
•EM•DB•AE=3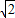
点评:本题考查的知识点是二面角的平面角求求法,棱锥的体积,空间中直线与直线的位置关系,(1)要熟练掌握空间线线垂直与线面垂直之间的相互转化,(2)的关键是构造出二面角的平面角,然后解三角形求出棱锥的棱长.

练习册系列答案
相关题目
 请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.
请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.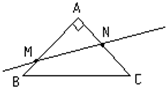 如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.
如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.
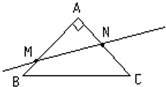 如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.
如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.