Question

已知函数f(x)＝lnx＋x². (1)若函数g(x)＝f(x)－ax在定义域内为增函数，求实数a的取值范围； (2)在(1)的条件下，若a>1，h(x)＝e^3x－3ae^x，x∈[0，ln2]，求h(x)的极小值； (3)设F(x)＝2f(x)－3x²－kx(k∈R)，若函数F(x)存在两个零点m，n(0<m<n)，且满足2x₀＝m＋n，问：函数F(x)在(x₀，F(x₀))处的切线能否平行于x轴？若能，求出该切线方程，若不能，请说明理由．

Answer 1

解：(1)g(x)＝f(x)－ax＝lnx＋x²－ax，g′(x)＝＋2x－a.

由题意，知g′(x)≥0对x∈(0，＋∞)恒成立，即a≤_min.

又x>0,2x＋≥2，当且仅当x＝时等号成立．

故_min＝2，所以a≤2.    ……3分

(2)由(1)知，1<a≤2.令e^x＝t，则t∈[1,2]，则h(x)＝H(t)＝t³－3at.

H′(t)＝3t²－3a＝3(t－)(t＋)．

由H′(t)＝0，得t＝或t＝－(舍去)，

∵a∈(1,2]，∴∈，

①若1<t≤，则H′(t)<0，H(t)单调递减，h(x)在(0，ln]也单调递减；

②若<t≤2，则H′(t)>0，H(t)单调递增，h(x)在[ln，ln2]也单调递增．

故h(x)的极小值为h(ln)＝－2a.  ……7分

(3)设F(x)在(x₀，F(x₀))处的切线平行于x轴，其中F(x)＝2lnx－x²－kx.

结合题意，有

①－②得2ln－(m＋n)(m－n)＝k(m－n)，所以k＝－2x₀.由④得k＝－2x₀，

所以ln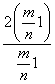＝＝.⑤

设u＝∈(0,1)，⑤式变为lnu－＝0(u∈(0,1))．

设y＝lnu－(u∈(0,1))，y′＝－＝＝>0，

所以函数y＝lnu－在(0,1)上单调递增，因此，y<y|_u＝1＝0，即lnu－<0.

也就是，ln<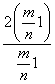，此式与⑤矛盾．

所以F(x)在(x₀，F(x₀))处的切线不能平行于x轴．