题目内容
等比数列{an}的各项均为正数,且a5a6+a4a7+a3a8=27,则log3a1+log3a2+log3a3+…+log3a10=( )
分析:由题设条件知a5a6=9,再由等比数列的性质知log3a1+log3a2+log3a3+…+log3a10=log3(a5a6)5,由此能求出结果.
解答:解:∵等比数列{an}的各项均为正数,且a5a6+a4a7+a3a8=27,
∴a5a6=a4a7=a3a8=9,
∴log3a1+log3a2+log3a3+…+log3a10
=log3(a1×a2×a3×…×a10)
=log3(a5a6)5
=log3310
=10.
故选B.
∴a5a6=a4a7=a3a8=9,
∴log3a1+log3a2+log3a3+…+log3a10
=log3(a1×a2×a3×…×a10)
=log3(a5a6)5
=log3310
=10.
故选B.
点评:本题考查等比数列的性质及其应用,解题时要注意对数性质的灵活运用,是基础题.

练习册系列答案
相关题目
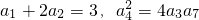 ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________. ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .