题目内容
已知一椭圆的两焦点为F1(0,-1)、F2(0,1),直线y=4是该椭圆的一条准线.(1)求此椭圆方程;
(2)设点P在椭圆上,且|PF1|-|PF2|=1,求tan∠F1PF2的值.
解:(1)设椭圆方程为![]() =1(a>b>0).
=1(a>b>0).
由题设知c=1,![]() =4,
=4,
∴a2=4,b2=a2-c2=3.
∴所求椭圆方程为![]() =1.
=1.
(2)由(1)知a2=4,a=2.
由椭圆定义知|PF1|+|PF2|=4,
又|PF1|-|PF2|=1,
∴|PF1|=![]() ,|PF2|=
,|PF2|=![]() .
.
又|F1F2|=2c=2,
由余弦定理cos∠F1PF2=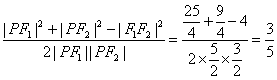 .
.
∵sin∠F1PF2=![]() ,∴tan∠F1PF2=
,∴tan∠F1PF2=![]() .
.

练习册系列答案
相关题目
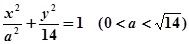 的两焦点为
的两焦点为 ,现将坐标平面沿
,现将坐标平面沿 轴折成二面角,二面角的度数为
轴折成二面角,二面角的度数为 ,已知折起后两焦点的距离
,已知折起后两焦点的距离 ,则满足题设的一组数值:
,则满足题设的一组数值:
 (只需写出一组就可以,不必写出所有情况)
(只需写出一组就可以,不必写出所有情况) 是椭圆
是椭圆 的两焦点,P是椭圆上任意一点,过一焦点引
的两焦点,P是椭圆上任意一点,过一焦点引 的外角平分线的垂线,垂足为Q,则动点Q的轨迹为 ( ▲ )
的外角平分线的垂线,垂足为Q,则动点Q的轨迹为 ( ▲ )